Hoje adiciono alguns comentários sobre a estratégia implementada nos últimos dois posts, aqui e aqui.
Para evitar ter que estimar tudo novamente, carrego uma tibble que contém apenas os resultados finais:
library(curl)
library(broom)
library(ggdist)
library(readxl)
library(lubridate)
library(tidyverse)
library(distributional)
url <- "https://github.com/Reckziegel/site/raw/master/data/momentum_ep"
data <- read_rds(url)
data
## # A tibble: 590 x 4
## .date `Momentum-EP` IBOV `One Over N`
## <date> <dbl> <dbl> <dbl>
## 1 2011-02-04 -0.0142 -0.0216 -0.0199
## 2 2011-02-11 0.00556 0.00742 0.0121
## 3 2011-02-18 0.0325 0.0345 0.0356
## 4 2011-02-25 -0.0214 -0.0172 -0.0297
## 5 2011-03-04 0.0267 0.0165 0.0214
## 6 2011-03-11 0.00138 -0.0197 -0.0126
## 7 2011-03-18 -0.00765 0.00292 0.000207
## 8 2011-03-25 0.0211 0.0132 0.0130
## 9 2011-04-01 0.0327 0.0219 0.0316
## 10 2011-04-08 -0.0148 -0.00797 -0.0148
## # ... with 580 more rows
Esse dadaset apresenta os retornos líquidos de custos operacionais - ao ano - tanto da estratégia de momentum entropy-pooling, quanto da famosa .
A performance cumulativa desses dois portfolios mais o Ibovespa pode ser vista com o comando abaixo:
data |>
# compound
mutate(across(where(is.numeric), ~ cumprod(1 + .x) * 100)) |>
# tidy data
pivot_longer(cols = -.date) |>
# plot
ggplot(aes(x = .date, y = value, color = name)) +
geom_line() +
scale_y_log10() +
scale_color_viridis_d(end = 0.75, option = "C") +
labs(title = "Corrida de Cavalos",
subtitle = "Momentum Entropy-Pooling vs. 1 / N",
x = NULL, y = NULL, color = NULL) +
theme(legend.position = "bottom")
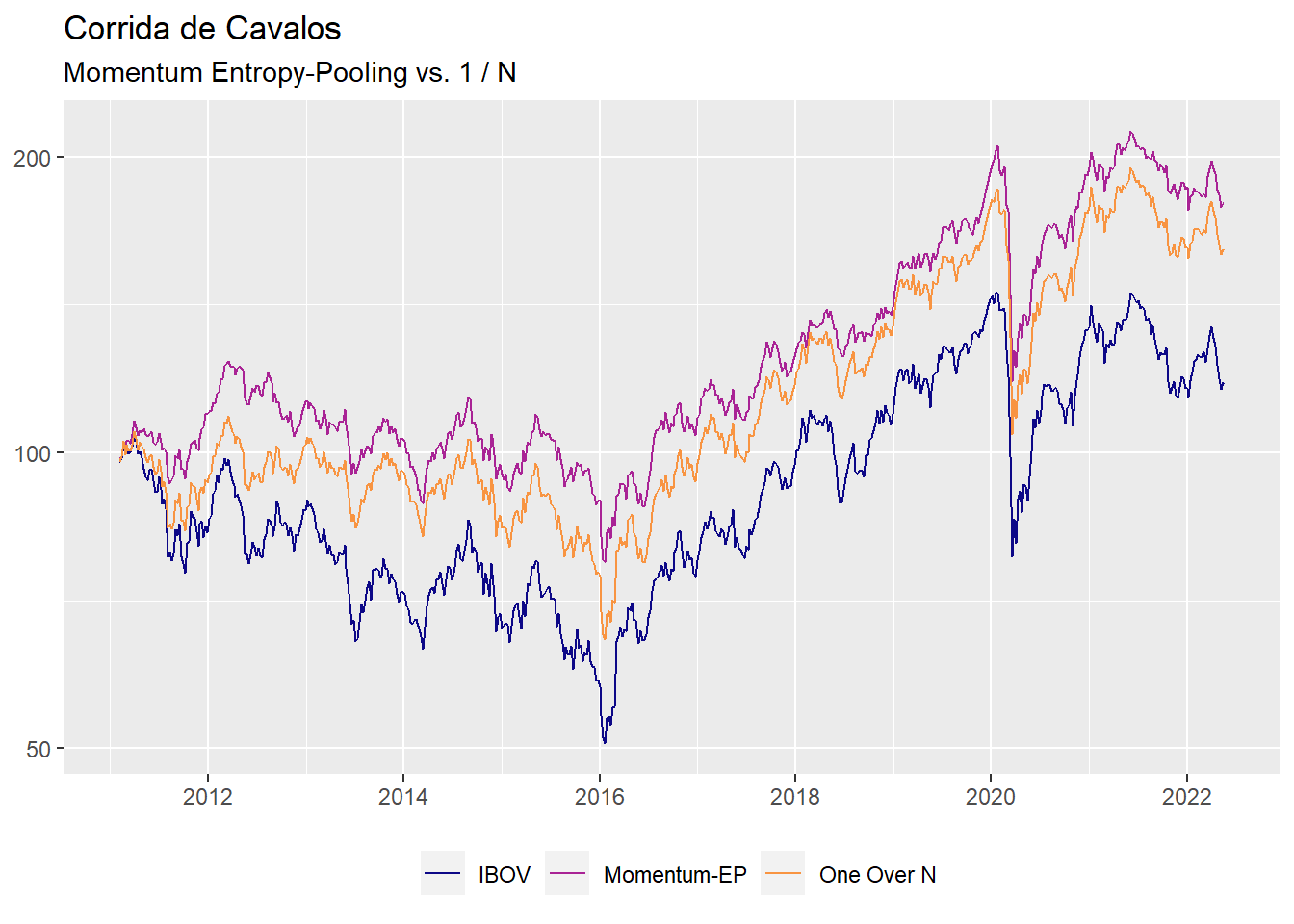
As estratégias “batem” o índice dentro do período selecionado, mas, como quase sempre, o portfolio é difícil de ser superado por uma larga margem.
Nesse caso, sempre há a possibilidade de que o excesso de retorno esteja vinculado a um nível de volatilidade mais elevado. Dessa forma, calculo o retorno médio por unidade de risco (uma medida unificada performance):
data |>
pivot_longer(cols = -.date, names_to = "portfolio") |>
group_by(portfolio) |>
summarise(sharpe = mean(value)/ sd(value)) |>
arrange(desc(sharpe))
## # A tibble: 3 x 2
## portfolio sharpe
## <chr> <dbl>
## 1 Momentum-EP 0.0520
## 2 One Over N 0.0429
## 3 IBOV 0.0247
Novamente, entropy-pooling e saem melhores do que o Ibovespa.
Se houvesse o desejo de controlar mais de perto a volatilidade, a função
ffp::view_on_volatility()poderia ser utilizada- veja o post Opiniões nas Volatilidades. Outra alternativa seria controlar a “Vol” por meio da calibragem do indicador de aversão à risco, , ou ainda, utilizando uma função de utilidade diferente da quadrática.
Infelizmente, muitos portfolios com tilt em momentum são conhecidos por apresentarem Tail Risk. Assim, calculo também o VaR histórico para cada estratégia aos níveis de 95% e 99% de confiança:
data |>
pivot_longer(cols = -.date, names_to = "portfolio") |>
group_by(portfolio) |>
summarise(`VaR (0.05%)` = quantile(value, 0.05),
`VaR (0.01%)` = quantile(value, 0.01)) |>
arrange(desc(`VaR (0.05%)`))
## # A tibble: 3 x 3
## portfolio `VaR (0.05%)` `VaR (0.01%)`
## <chr> <dbl> <dbl>
## 1 Momentum-EP -0.0366 -0.0601
## 2 One Over N -0.0396 -0.0766
## 3 IBOV -0.0473 -0.0805
E, mais uma vez, entropy-pooling e possuem estatisticas melhores do que o Ibovespa.
É legítimo se questionar o porquê de investir tempo em research se a estratégia performa quase tão bem quanto entropy-pooling e não requer otimização, nem pesquisa adicional. Acho que a resposta para esse ponto passa pelo fato de que nem todos os retornos são feitos iguais.
Abaixo faço uma análise ex-post dos fatores de risco de cada estratégia para toda a amostra:
urls <- list(market = "https://nefin.com.br/resources/risk_factors/Market_Factor.xls",
smb = "https://nefin.com.br/resources/risk_factors/SMB_Factor.xls",
hml = "https://nefin.com.br/resources/risk_factors/HML_Factor.xls",
wml = "https://nefin.com.br/resources/risk_factors/WML_Factor.xls",
iml = "https://nefin.com.br/resources/risk_factors/IML_Factor.xls")
destfiles <- list("market.xls", "smb.xls", "hml.xls", "wml.xls", "iml.xls")
risk_factors <- map2(.x = urls,
.y = destfiles,
.f = ~ curl_download(url = .x, destfile = .y)) |>
map(read_excel) |>
reduce(left_join, by = c("year", "month", "day")) |>
mutate(date = make_date(year = year, month = month, day = day)) |>
rename_all(str_to_lower) |>
rename(rm = "rm_minus_rf") |>
select(date, everything(), -year, -month, -day)
data <- left_join(data, risk_factors, by = c(".date" = "date")) |>
na.omit()
# OLS Formulation
fml_ibov <- as.formula(IBOV ~ rm + smb + hml + wml + iml)
fml_ep <- as.formula(`Momentum-EP` ~ rm + smb + hml + wml + iml)
fml_oon <- as.formula(`One Over N` ~ rm + smb + hml + wml + iml)
unconditional <- lm(formula = fml_ibov, data = data) |>
tidy() |>
mutate(Cenário = "Ibovespa")
momentum_ep <- lm(formula = fml_ep, data = data) |>
tidy() |>
mutate(Cenário = "Momentum EP")
one_over_n <- lm(formula = fml_oon, data = data) |>
tidy() |>
mutate(Cenário = "One Over N")
regression <- bind_rows(unconditional, momentum_ep, one_over_n)
regression |>
mutate(term = fct_reorder(as_factor(term), estimate)) |>
filter(term != "(Intercept)") |>
ggplot(aes(y = term, group = `Cenário`, color = `Cenário`, fill = `Cenário`) ) +
stat_halfeye(aes(
xdist = dist_student_t(df = 2784, mu = estimate, sigma = std.error)), alpha = 0.75
) +
geom_vline(xintercept = 0, size = 1, color = "grey", linetype = 2) +
scale_fill_viridis_d(end = 0.75, option = "C") +
scale_color_viridis_d(end = 0.75, option = "C") +
scale_x_continuous(labels = scales::percent_format()) +
theme(legend.position = "bottom") +
labs(title = "Exposições Ex-Post",
subtitle = "Risk Drivers das Diferentes Estratégias",
x = NULL,
y = NULL)
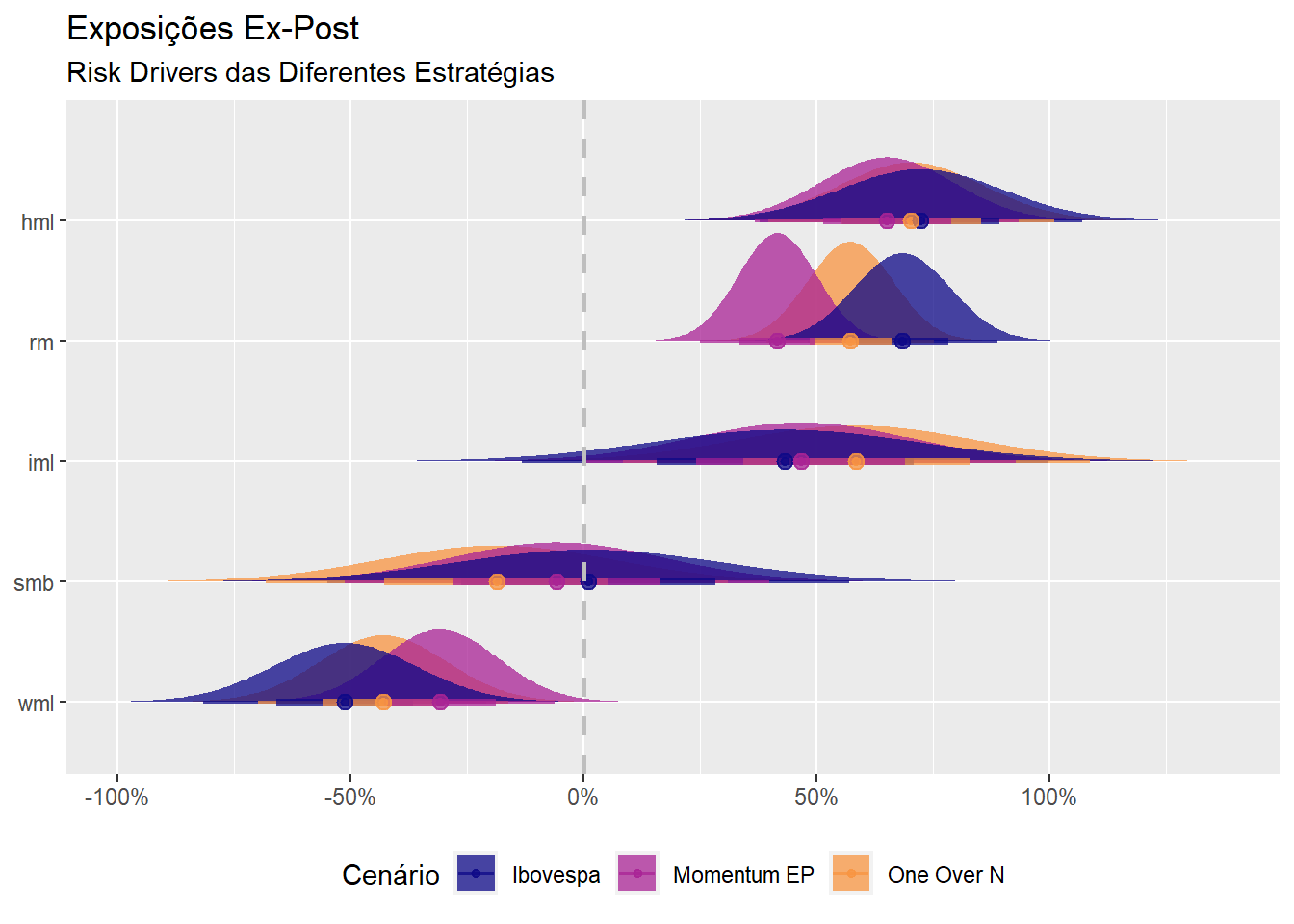
Como se esperava, a estratégia via entropy-pooling é mais bem sucedida do que no sentido de “puxar” os retornos em direção do fator de momentum, embora a exposição média ainda seja negativa (um problema potencialmente relacionado ao dataset de pequena dimensão que foi utilizado).
Uma agradável surpresa vem do fato que o risco de mercado é menor em entropy-pooling. Esse é justamente o tipo de benefício que se espera de uma estratégia sistemática.