Nos posts anteriores mostrei como utilizar a biblioteca ffp para adicionar opiniões em diversos elementos das distribuições multivariadas (retornos, volatilidades, correlações, margens, copulas, etc.). Hoje mostro como a abordagem das probabilidades flexíveis pode ser útil para condicionar os betas das regressões lineares.

Os pacotes utilizados são:

library(tidyverse)      # Onde tudo é mais fácil...
library(lubridate)      # Manipulação de datas
library(quantmod)       # Download de dados financeiros
library(timetk)         # Coerção entre diferentes estruturas 
library(readxl)         # Leitura de arquivos em excel
library(broom)          # Visualização das Regressões
library(ggdist)         # Visualização das Regressões
library(distributional) # Visualização das Regressões
library(ffp)            # Probabilidades Flexíveis

Deixo de lado o dataset EuStockMarkets para brincar um pouquinho com o ibovespa e os risk-factors calculados pelo time do NEFIN.

Os dados do índice Ibovespa são coletados diretamente via Yahoo Finance:

ibov <- getSymbols(Symbols = "^BVSP", auto.assign = FALSE) |> 
  tk_tbl(preserve_index = TRUE, rename_index = "date") |> 
  select(date, ibov = contains("Adjusted")) |> 
  transmute(date, ibov = c(0, diff(log(ibov))))
ibov

## # A tibble: 3,809 x 2
##    date           ibov
##    <date>        <dbl>
##  1 2007-01-02  0      
##  2 2007-01-03 -0.0209 
##  3 2007-01-04 -0.00961
##  4 2007-01-05 -0.0412 
##  5 2007-01-08  0.0138 
##  6 2007-01-09 -0.0194 
##  7 2007-01-10  0.00780
##  8 2007-01-11  0.00786
##  9 2007-01-12  0.00991
## 10 2007-01-15 -0.00409
## # ... with 3,799 more rows

Já os dados do NEFIN ficam disponíveis no endereço https://nefin.com.br/data/risk_factors.html. Esse link contém url’s estáveis, o que facilita o download das informações:

urls <- list(market = "https://nefin.com.br/resources/risk_factors/Market_Factor.xls",
             smb    = "https://nefin.com.br/resources/risk_factors/SMB_Factor.xls",
             hml    = "https://nefin.com.br/resources/risk_factors/HML_Factor.xls",
             wml    = "https://nefin.com.br/resources/risk_factors/WML_Factor.xls",
             iml    = "https://nefin.com.br/resources/risk_factors/IML_Factor.xls",
             risk_free = "https://nefin.com.br/resources/risk_factors/Risk_Free.xls")

destfiles <- list("market.xls", "smb.xls", "hml.xls", "wml.xls", "iml.xls", "risk_free.xls")

risk_factors <- map2(.x = urls,
                     .y = destfiles,
                     .f = ~ curl::curl_download(url = .x, destfile = .y)) |> 
  map(read_excel) |> 
  reduce(left_join, by = c("year", "month", "day")) |> 
  mutate(date = make_date(year = year, month = month, day = day)) |> 
  rename_all(str_to_lower) |> 
  rename(rm = "rm_minus_rf", rf = "risk_free") |> 
  select(date, everything(), -year, -month, -day, -rf)
risk_factors

## # A tibble: 5,278 x 6
##    date              rm        smb       hml       wml      iml
##    <date>         <dbl>      <dbl>     <dbl>     <dbl>    <dbl>
##  1 2001-01-02  0.00660   0.000524   0.0655   -0.00631   0.0141 
##  2 2001-01-03  0.0624    0.00539    0.00939  -0.0286    0.00451
##  3 2001-01-04 -0.000310  0.00669   -0.00233  -0.000946 -0.00923
##  4 2001-01-05 -0.0128    0.00352   -0.00240   0.00598   0.0251 
##  5 2001-01-08  0.00398   0.00788    0.00195  -0.00410  -0.00118
##  6 2001-01-09  0.0200    0.00593   -0.000916  0.00956  -0.00398
##  7 2001-01-10 -0.00437   0.0132     0.0125   -0.000691  0.0221 
##  8 2001-01-11  0.00469  -0.0108    -0.00345  -0.00306  -0.00228
##  9 2001-01-12 -0.00678   0.00662    0.00347   0.00602   0.0103 
## 10 2001-01-15  0.00511   0.0000672 -0.000760 -0.0138    0.00689
## # ... with 5,268 more rows

A etapa de coleta é finalizada com a unificação dos objetos ibov e risk_factors em uma única tibble, que contem os retornos de 03-01-2012 até 29-04-2022:

data <- left_join(ibov, risk_factors, by = "date") |> 
  filter(date > "2010-01-02") |> 
  na.omit()
data

## # A tibble: 3,037 x 7
##    date           ibov       rm      smb        hml      wml       iml
##    <date>        <dbl>    <dbl>    <dbl>      <dbl>    <dbl>     <dbl>
##  1 2010-01-04  0.0210   0.0214  -0.00544  0.00345   -0.00640 -0.00615 
##  2 2010-01-05  0.00278  0.00133 -0.00411  0.00497   -0.00674  0.00249 
##  3 2010-01-06  0.00694  0.00587  0.0144   0.00473    0.00624  0.00883 
##  4 2010-01-07 -0.00394 -0.00295  0.00984  0.00533    0.00367  0.0130  
##  5 2010-01-08 -0.00267 -0.00184  0.00961 -0.0000292 -0.00294  0.0172  
##  6 2010-01-11  0.00242  0.00147  0.0100   0.0123     0.00545  0.0192  
##  7 2010-01-12 -0.00508 -0.00465  0.00351 -0.00348    0.00184 -0.00559 
##  8 2010-01-13  0.00440  0.00400  0.00639  0.00147    0.00633  0.000103
##  9 2010-01-14 -0.00833 -0.00697 -0.00107 -0.00835    0.00638  0.00515 
## 10 2010-01-15 -0.0119  -0.0122   0.00950  0.00979    0.00972  0.0108  
## # ... with 3,027 more rows

Com isso, o foco se direciona para o computo das opiniões. Utilizo dois métodos que estão no pacote ffp e ainda não foram discutidos nos posts anteriors: crisp e exp_decay.

O objetivo da função crisp é restringir a análise para alguma situação macro/micro específica, dando \(100\%\) de peso para as condições que atendem a uma certa restrição e \(0\%\) para aquelas não atendem:

$$p = \begin{cases} 1 & \text{se } x_t \text{ atende a restrição} \\ 0 & \text{se } x_t \text{ não atende a restrição} \end{cases}$$

Uma vez que as dummies sejam computadas, o vetor \(p\) é normalizado para garantir que a soma do processo seja igual a \(1\).

crisp_positive <- crisp(data$ibov, data$ibov > 0)
crisp_negative <- crisp(data$ibov, data$ibov < 0)

No exemplo acima, a análise é condicionada para os períodos em que o ibovespa teve retornos acima e abaixo de zero.

Já a função exp_decay busca dar mais relevância para observações recentes por meio da relação de alisamento exponencial:

$$ p = e^{-\lambda(T-t)}$$ Em que \(\lambda\) é um parâmetro de decaimento que determina o grau de persistência das últimas observações. Via de regra, quando maior o parâmetro \(\lambda\), menor o número de cenários efetivamente considerados. Utilizo \(\lambda = 0.001359\), cuja a meia vida é próxima de 2 anos¹:

exp_smoothing  <- exp_decay(data$ibov, 0.001359)

Com base nessas opiniões - ou qualquer outro vetor de probabilidades que você queira - é possível estimar os betas condicionais. A função lm possui um argumento pouco conhecido, mas incrivelmente útil, chamado weights. Quando esse argumento não é nulo, a função lm conduz a estimação por meio dos mínimos quadrados ponderados (MQP), de modo que as observações com maior peso ganham maior importância no processo de otimização.

Uso essa ideia para uma análise de atribuição ex-post do ibovespa:

fml <- as.formula(ibov ~ rm + smb + hml + wml + iml)

unconditional <- lm(formula = fml, data = data) |> 
  tidy() |> 
  mutate(Cenário = "Incondicional")

positive <- lm(formula = fml, data = data, weights = crisp_positive) |> 
  tidy() |> 
  mutate(Cenário = "Otimista")

negative <- lm(formula = fml, data = data, weights = crisp_negative) |> 
  tidy() |> 
  mutate(Cenário = "Pessimista")

exponential <- lm(formula = fml, data = data, weights = exp_smoothing) |> 
  tidy() |> 
  mutate(Cenário = "Exponencial")

regression <- bind_rows(unconditional, positive, negative, exponential)
regression

## # A tibble: 24 x 6
##    term         estimate std.error statistic   p.value Cenário      
##    <chr>           <dbl>     <dbl>     <dbl>     <dbl> <chr>        
##  1 (Intercept)  0.000168 0.0000429      3.91 9.35e-  5 Incondicional
##  2 rm           1.05     0.00351      300.   0         Incondicional
##  3 smb          0.130    0.00968       13.4  6.15e- 40 Incondicional
##  4 hml          0.0788   0.00607       13.0  1.48e- 37 Incondicional
##  5 wml         -0.0577   0.00470      -12.3  9.14e- 34 Incondicional
##  6 iml         -0.227    0.0103       -22.1  4.00e-100 Incondicional
##  7 (Intercept)  0.00108  0.0000604     17.9  4.60e- 68 Otimista     
##  8 rm           0.992    0.00483      205.   0         Otimista     
##  9 smb          0.112    0.00968       11.6  1.90e- 30 Otimista     
## 10 hml          0.0705   0.00598       11.8  2.25e- 31 Otimista     
## # ... with 14 more rows

regression  |> 
  mutate(term = fct_reorder(as_factor(term), estimate)) |> 
  filter(term != "rm", term != "(Intercept)") |> 
  ggplot(aes(y = term, group = `Cenário`, color = `Cenário`, fill = `Cenário`) ) +
  stat_halfeye(aes(
    xdist = dist_student_t(df = 2784, mu = estimate, sigma = std.error)), alpha = 0.75
    ) + 
  geom_vline(xintercept = 0, size = 1, color = "grey", linetype = 2) + 
  scale_fill_viridis_d(end = 0.75, option = "C") + 
  scale_color_viridis_d(end = 0.75, option = "C") + 
  theme(legend.position = "bottom") + 
  labs(title    = "Regressão Linear via MQP-Entropy-Pooling",
       subtitle = "Distribuição dos parâmetros estimados sob diferentes cenários",
       x        = NULL, 
       y        = NULL)

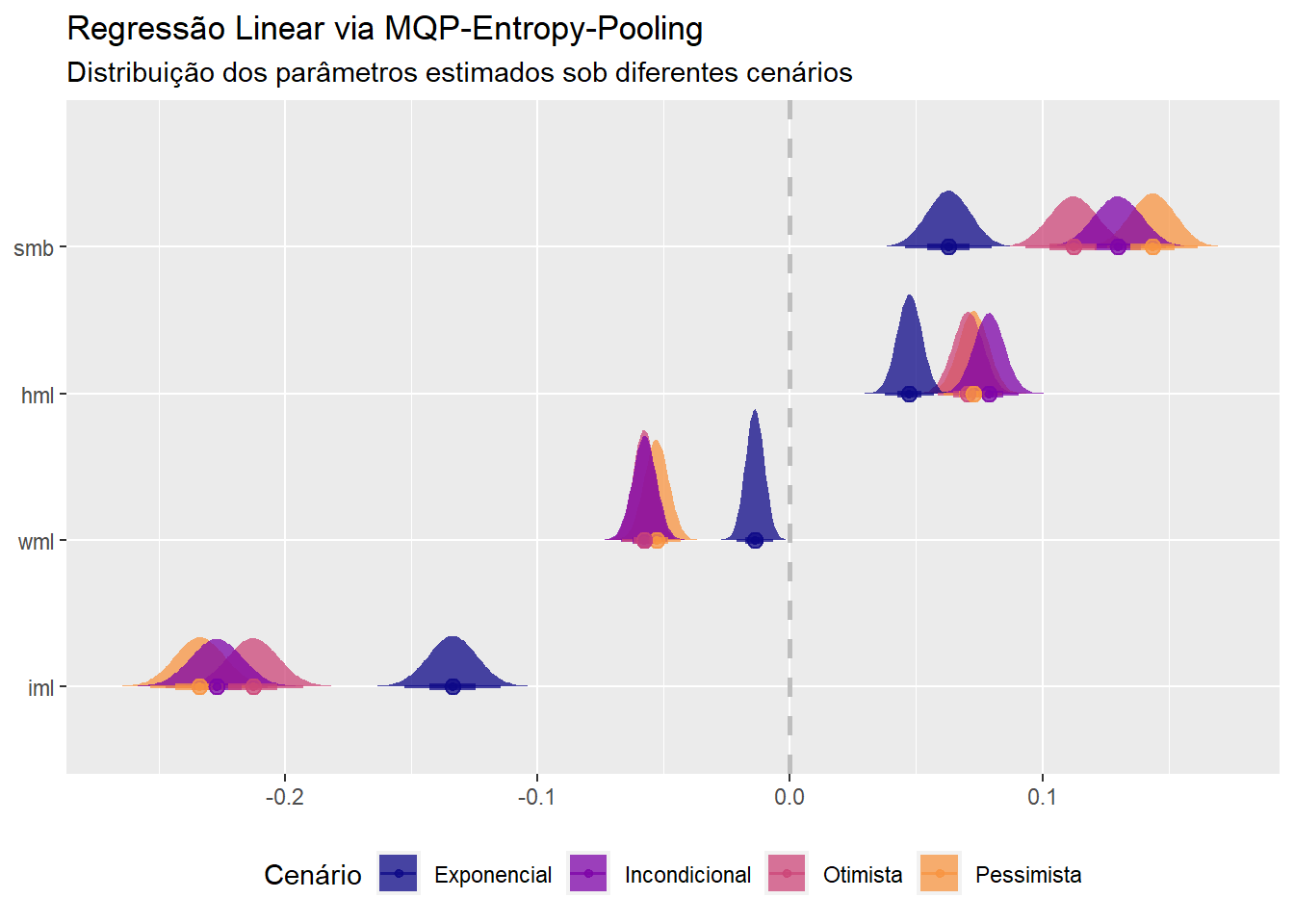
A grosso modo, o Ibovespa é um índice com um tilt em direção a empresas de value com média capitalização. A entrada de novas companhias e a diminuição da importância de empresas tradicionais (PETR4, VALE3, BBAS3, etc.) acho que explica parcialmente o direcionamento em relação ao fator SMB. A exposição a momentum é baixa e a liquidez média bastante elevada (prêmio de iliquidez negativo).

Sob o cenário definido como “pessimista”, o Ibovespa parece ficar ainda mais exposto ao fator SMB, possivelmente porque em momentos de sell-off as empresas cíclicas domésticas (que têm menor capitalização) são as primeiras a tomar porrada. Já no cenário “otimista”, o drift em direção as empresas de baixa capitalização diminui e a liquidez aumenta, sem muito impacto sobre os demais fatores. Por fim, chama atenção como a performance recente - “exponencial” - diverge do comportamento médio dos últimos \(10\) anos.

Bacana ver como uma análise que começa de maneira totalmente bayesiana consegue conversar com o mundo frequentista de maneira rápida e sem complicações.