Vamos assumir que o time de gestão esteja receoso com a performance futura do mercado de ações e deseje simular um cenário de “estresse” para medir o impacto ex-ante sobre o P&L.
Uma das maneiras de simular esse tipo de comportamento é colocando as opiniões nas correlações - como fiz aqui - ou manipulando as copulas diretamente. No post de hoje mostro como implementar o segundo approach.
Como de praxe, análise é conduzida com o dataset EuStockMarkets, que vem com a instalação do R:
# invariance
x <- matrix(diff(log(EuStockMarkets)), ncol = 4)
colnames(x) <- colnames(EuStockMarkets)
head(x)
## DAX SMI CAC FTSE
## [1,] -0.009326550 0.006178360 -0.012658756 0.006770286
## [2,] -0.004422175 -0.005880448 -0.018740638 -0.004889587
## [3,] 0.009003794 0.003271184 -0.005779182 0.009027020
## [4,] -0.001778217 0.001483372 0.008743353 0.005771847
## [5,] -0.004676712 -0.008933417 -0.005120160 -0.007230164
## [6,] 0.012427042 0.006737244 0.011714353 0.008517217
No gráfico abaixo coloco o índice SMI no eixo x e o DAX no eixo y. Perceba que é a combinação das distribuições marginais que nos permite fazer inferência sobre a associação linear dessas variáveis:
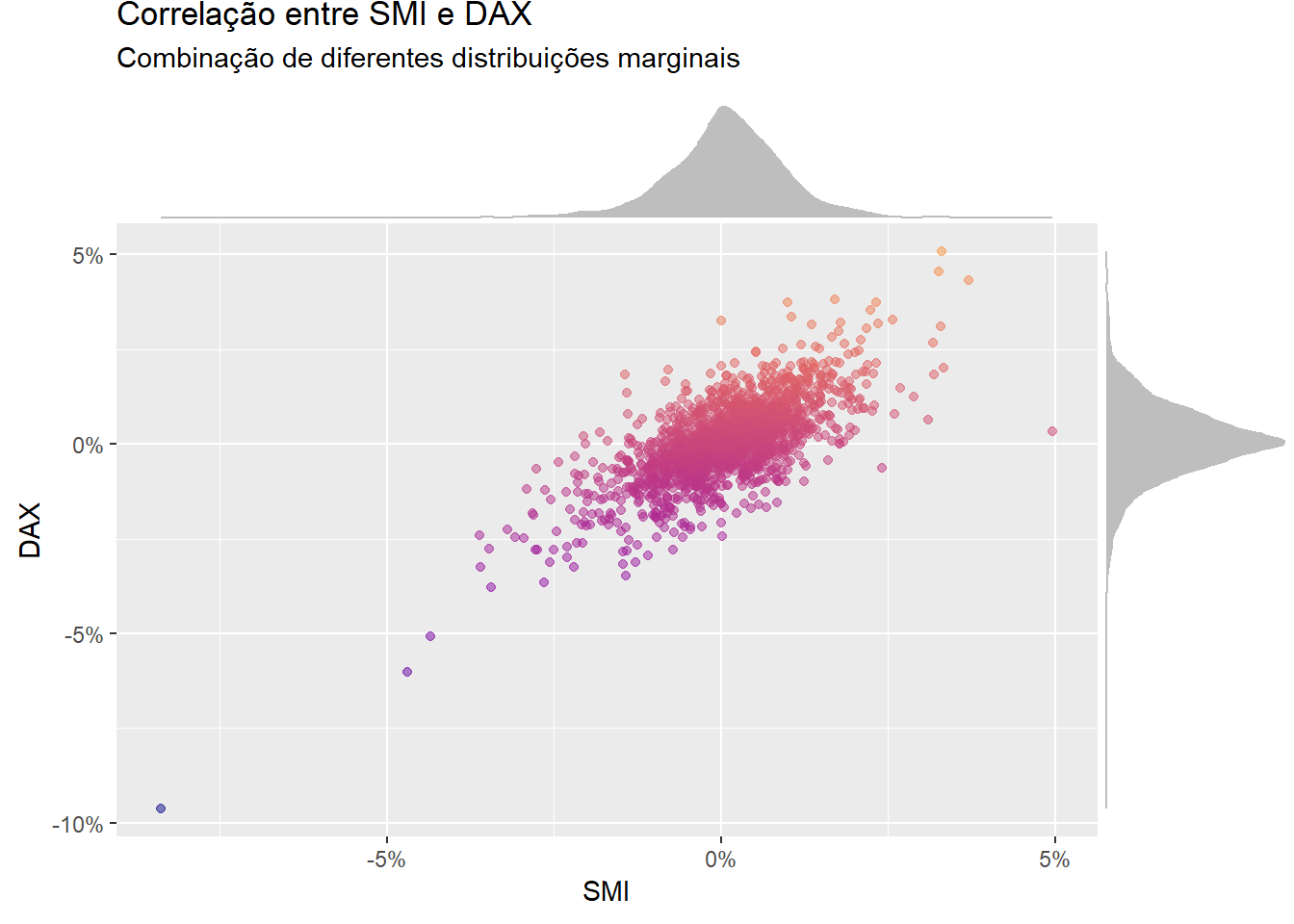
Ou seja, são as informações individuais - as “margens” - que ditam a estrutura de correlação dos ativos financeiros.
Distribuição Multivariada = Margens + Copulas
As margens carregam as informações puramente índividuais (exclusivas de cada ativo), enquanto as copulas levam as informações puramente conjuntas (de dependência entre as variáveis)1.
Manipulando a expressão acima obtemos:
Copulas = Distribuição Multivariada - Margens
Em outras palavras, a copula é a informação que sobra uma vez que tenhamos “limpado” a informação puramente individual contida nas margens.
Abaixo a copula empírica dos índices SMI e DAX:
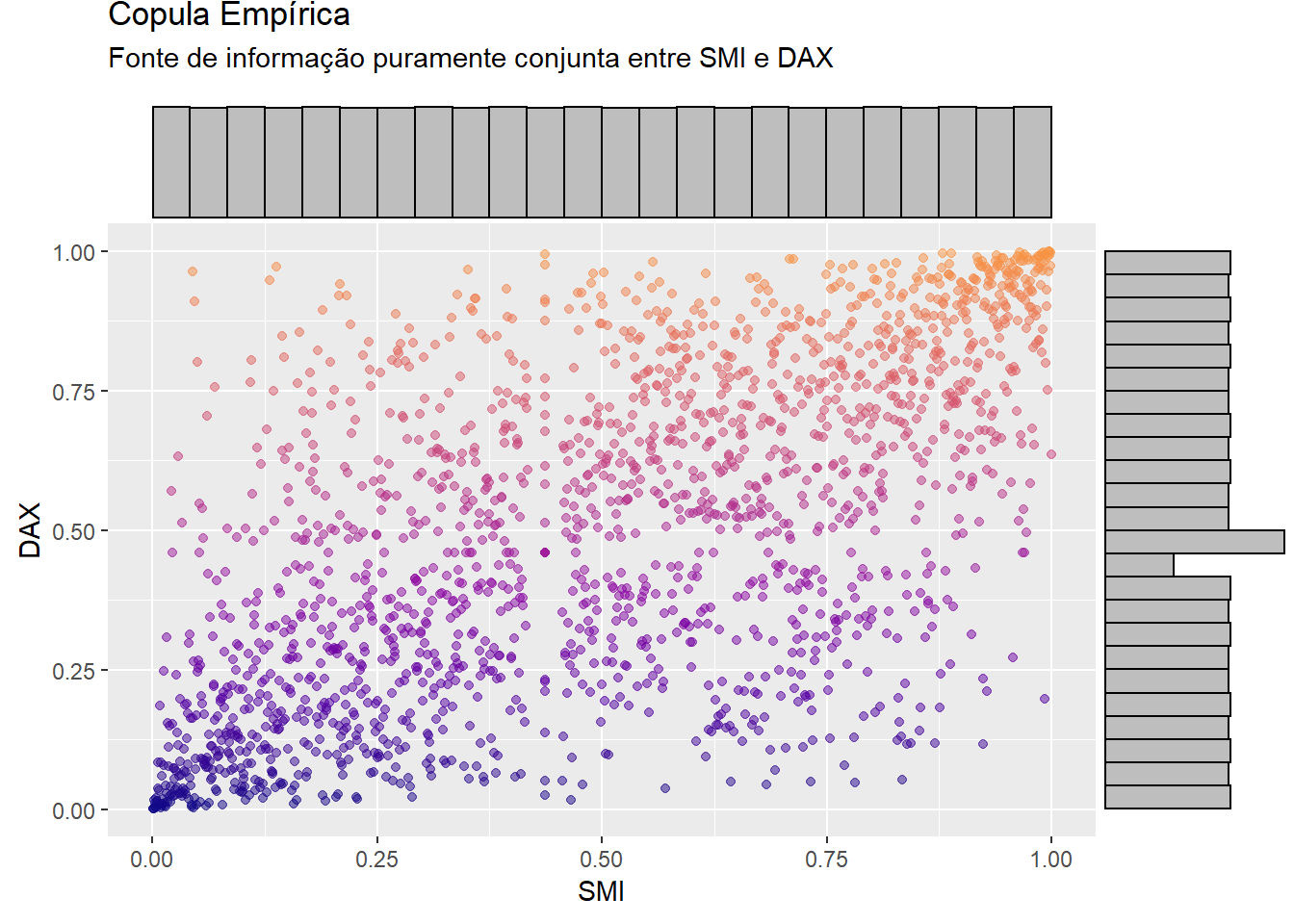
Perceba que essa copula, em particular, apresenta dois pontos de aglomeração nos extremos: quando o SMI cai muito (perto de \(0\)), o DAX também cai muito (perto de \(0\)); quando SMI sobe muito (perto de \(1\)), o DAX também sobe muito (perto de \(1\)). Ou seja, essa copula está revelando que em momentos de euforia e pânico os índices SMI e DAX andam juntos!
Obviamente, nem todas as copulas são iguais. Abaixo mostro quatro tipos de copulas bastante conhecidas, que fazem parte do mundo arquimediano.

A copula de Clayton geralmente é utilizada para modelar eventos de pânico, porque uma enorme quantidade de pontos se aglomeram à esquerda na parte inferior (quando x cai, y também cai). Já a copula de Gumbel é utilizada para modelar eventos de euforia, pois muitos pontos se concentram à direita na parte superior (quando x sobe, y também sobe).
Na prática, não há uma única forma de “decompor” as distribuições entre margens e copulas. Aqui, sigo o approach das probabilidades flexíveis e manipulo esses elementos com o algoritmo CMA, que oferece uma receita não-paramétrica de dois passos para “separar” e “combinar” distribuições multivariadas.
O pacote cma não está no CRAN, então para reproduzir os códigos abaixo você deve rodar o comando: devtools::install_github("Reckziegel/CMA") no console:
# devtools::install_github("Reckziegel/CMA")
library(cma)
sep <- cma_separation(x = x)
sep
## # CMA Decomposition
## marginal: << tbl 1859 x 4 >>
## cdf : << tbl 1859 x 4 >>
## copula : << tbl 1859 x 4 >>
Para objetos da classe cma_separation o pacote cma disponibiliza a família de funções fit_copula_*(). Como comentei, a copula de clayton é um candidado natural para modelar eventos de estresse:
clayton_fit <- fit_copula_clayton(copula = sep, method = "ml")
clayton_fit
## # New Copula
## Conveged: 0
## Dimension: 4
## Log-Likelihood: 1615.755
## Model: claytonCopula
Perceba que nessa copula apenas um parâmetro precisa ser estimado:
clayton_fit$estimate
## [1] 1.066038
Quando maior for o parâmetro \(\alpha\), mais aglomerados os dados ficam a esquerda da distribuição. Veja:
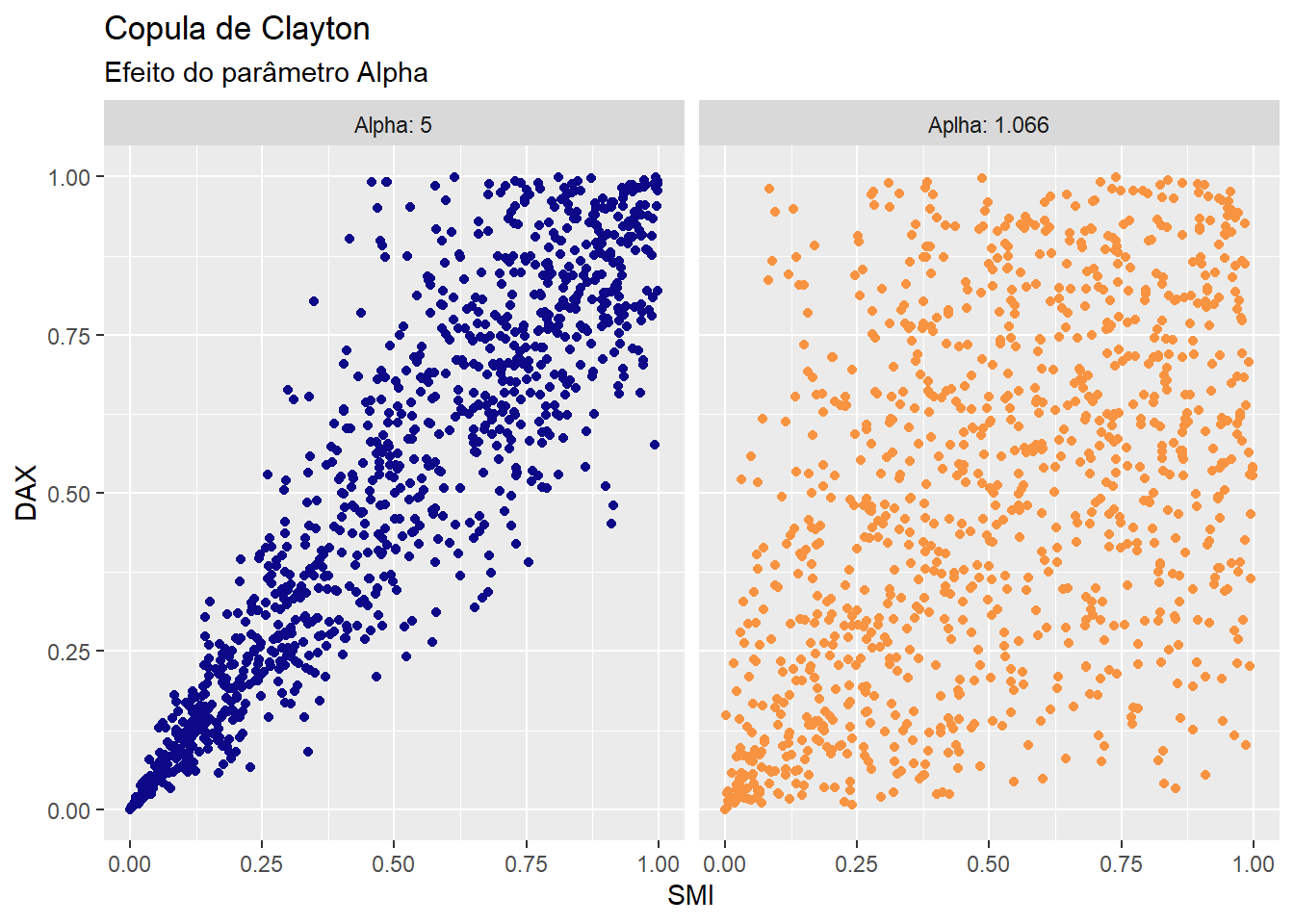
Para precificar um cenário de “sell-off” ex-ante, adiciono uma perturbação no parâmetro \(\alpha\). Em particular, uso \(\alpha = 5\) e com essa nova estimativa simulo um painel com \(1.000.000\) de linhas e \(4\) colunas que guardam as mesmas propriedades estatísticas do objeto clayton_fit.
Esse processo é realizado com a função generate_copulas:
# lock environment
set.seed(2)
# "twick" the alpha parameter
clayton_fit$estimate <- 5
# generate new scenarios
simul_clayton <- generate_copulas(model = clayton_fit, n = 1000000)
Para colocar opiniões nas copulas, o pacote ffp disponibiliza a função view_on_copula:
library(ffp)
prior_for_simul <- rep(1 / 1000000, 1000000)
views_on_cop <- view_on_copula(
x = sep$copula,
simul = simul_clayton,
p = prior_for_simul
)
views_on_cop
## # ffp view
## Type: View On Copula
## Aeq : Dim 34 x 1859
## beq : Dim 34 x 1
Formalmente, o objetivo é minimizar a expressão:
$$ min \sum_{i=1}^I x_i(ln(x_i) - ln(p_i)) $$
\(s.a.\)
$$ \sum_{i=1}^I \hat{p_i} U_{j,k}U_{j,l} = \sum_{i=1}^I p_i \hat{U}_{j,k}\hat{U}_{j,l} $$
$$ \sum_{i=1}^I \hat{p_i} U_{j,k}U_{j,l}U_{j,i} = \sum_{i=1}^I p_i \hat{U}_{j,k}\hat{U}_{j,l}\hat{U}_{j,i} $$
$$ \sum_{i=1}^I \hat{p_i} U_{j,k} = 0.5 $$
$$ \sum_{i=1}^I \hat{p_i} U_{j,k}^2 = 0.33 $$
No qual \(p_i \hat{U}_{j,k}\hat{U}_{j,l}\) e \(p_i \hat{U}_{j,k}\hat{U}_{j,l}\hat{U}_{j,i}\) atuam como restrições nos momentos cruzados e \(0.5\) e \(0.33\) condicionam os dois primeiros momentos da distribuição uniforme.
Esse sistema é solucionado com a função entropy_pooling:
prior_from_data <- rep(1 / nrow(x), nrow(x))
ep <- entropy_pooling(
p = prior_from_data,
Aeq = views_on_cop$Aeq,
beq = views_on_cop$beq,
solver = "nloptr"
)
ep
## <ffp[1859]>
## 2.675292e-12 0.0002722608 6.850905e-06 5.248376e-05 0.001002795 ... 0.0005913308
O vetor de probabilidades ep é aquele que consegue atender as opiniões do econometrista distorcendo ao mínimo as probabilidades uniformes:
library(ggplot2)
autoplot(ep) +
scale_color_viridis_c(option = "C", end = 0.75) +
labs(title = "Distribuição de Probabilidades Posteriores",
subtitle = "Perturbação na Copula de Clayton",
x = NULL,
y = NULL)
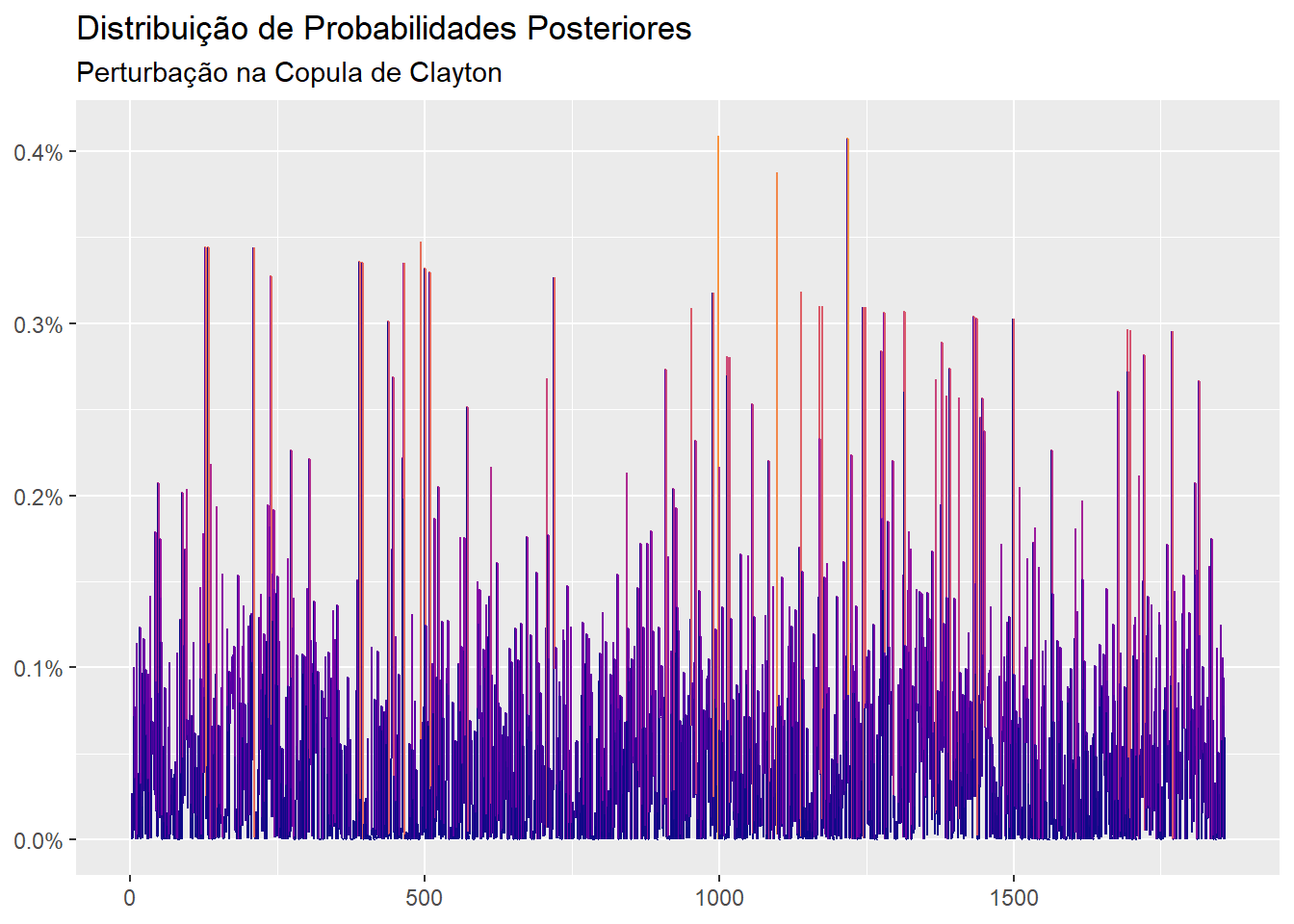
Dessas probabilidades, deriva-se os momentos condicionais, que são o principal insumo para construção de uma fronteira eficiente bayesiana:
ffp_moments(x = x, p = ep)
## $mu
## DAX SMI CAC FTSE
## 0.0005338149 0.0004894317 0.0004274987 0.0004413356
##
## $sigma
## DAX SMI CAC FTSE
## DAX 1.194373e-04 9.354658e-05 1.070850e-04 7.536304e-05
## SMI 9.354658e-05 9.929703e-05 9.467923e-05 6.690249e-05
## CAC 1.070850e-04 9.467923e-05 1.314587e-04 8.035356e-05
## FTSE 7.536304e-05 6.690249e-05 8.035356e-05 7.180174e-05
Uma maneira simples de analisar o impacto dessas opiniões nos ativos da carteira é combinando o output da função empirical_stats com o ggplot2:
library(dplyr)
prior <- empirical_stats(x = x, p = as_ffp(prior_from_data)) |>
mutate(type = "Prior")
posterior <- empirical_stats(x = x, p = ep) |>
mutate(type = "Posterior")
bind_rows(prior, posterior) |>
ggplot(aes(x = name, y = value, color = type, fill = type)) +
geom_col(position = "dodge") +
facet_wrap(~stat, scales = "free") +
scale_fill_viridis_d(end = 0.75, option = "C") +
scale_color_viridis_d(end = 0.75, option = "C") +
labs(title = "Análise de 'Estresse' ex-ante via Entropy-Pooling",
subtitle = "Perturbação na Copula de Clayton",
x = NULL, y = NULL, color = NULL, fill = NULL)
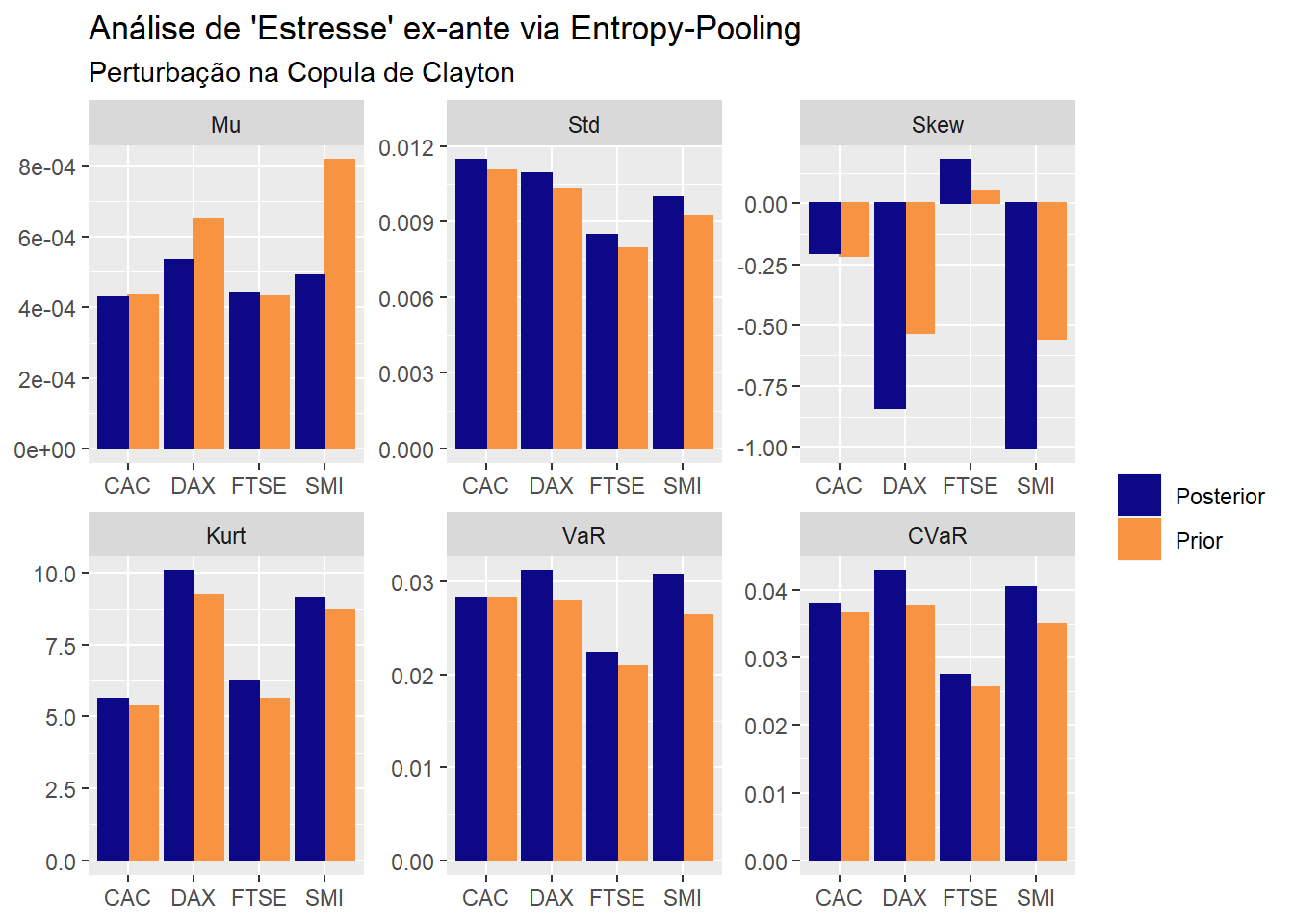
Perceba que o impacto da perturbação vai na direção esperada: sob regime de “stress” os retornos são menores, as volatilidades mais elevadas, as margens mais assimétricas, as caudas mais largas e, por fim, o VaR e Expected Shortfall também são maiores.
Manipulando os objetos prior e posterior é possível computar o impacto exato sobre qualquer uma dessas estatísticas. Por exemplo, o incremento no Value-at-Risk (VaR), ao nível de \(99\%\), pode ser calculado da seguinte forma:
library(tidyr)
bind_rows(prior, posterior) |>
filter(stat == "VaR") |>
select(name, value, type) |>
pivot_wider(names_from = "type", values_from = "value") |>
transmute(
Ativo = name,
`VaR: Diferença Anualizada` = paste0(round(100 * sqrt(252) * (Posterior - Prior), 2), "%")
)
## # A tibble: 4 x 2
## Ativo `VaR: Diferença Anualizada`
## <chr> <chr>
## 1 DAX 5.12%
## 2 SMI 7.01%
## 3 CAC 0.02%
## 4 FTSE 2.28%
Por hoje é isso e no próximo post falarei sobre como modelar eventos de pânico com mixtures.