Dando sequência aos posts anteriores, hoje mostro como construir opiniões nas distribuições marginais.
Mais uma vez utilizo o dataset EuStockMarkets - que acompanha a instalação do R - para facilitar a reprodução dos resultados:
x <- diff(log(EuStockMarkets))
head(x)
## DAX SMI CAC FTSE
## [1,] -0.009326550 0.006178360 -0.012658756 0.006770286
## [2,] -0.004422175 -0.005880448 -0.018740638 -0.004889587
## [3,] 0.009003794 0.003271184 -0.005779182 0.009027020
## [4,] -0.001778217 0.001483372 0.008743353 0.005771847
## [5,] -0.004676712 -0.008933417 -0.005120160 -0.007230164
## [6,] 0.012427042 0.006737244 0.011714353 0.008517217
Vamos assumir que o time de econometria (após algumas linhas de código e meia dúzia de derivadas) conclua que a distribuição Student-t assimétrica é a que melhor se adapta aos dados em questão.
Para conduzir o processo de estimação utilizo o pacote cma1. Essa biblioteca não está no CRAN - for now - e para instala-la você deverá rodar o comando devtools::install_github("Reckziegel/CMA") no console:
# devtools::install_github("Reckziegel/CMA")
library(cma)
t_model <- fit_t(x, symmetric = FALSE)
t_model
## # Margins Estimation
## Converged: TRUE
## Dimension: 4
## AIC: -52711.16
## Log-Likelihood: 26374.58
## Model: Asymmetric Student-t
O pacote cma fornece algumas funções interessantes para geração de cenários. Utilizo generate_margins para criar um painel gigante com as mesmas propriedades estatísticas presentes em t_model:
set.seed(123)
t_margins <- generate_margins(model = t_model, n = 1000000)
t_margins
## # New Margins
## marginal: << tbl 1000000 x 4 >>
O output de t_margins é uma lista - tibble - que contém \(1.000.000\) linhas e \(4\) colunas. Veja:
t_margins$marginal
## # A tibble: 1,000,000 x 4
## DAX SMI CAC FTSE
## <dbl> <dbl> <dbl> <dbl>
## 1 -0.00549 -0.0101 -0.00796 -0.00802
## 2 -0.00334 0.0109 0.00599 -0.00564
## 3 0.0152 0.00675 0.0110 0.0112
## 4 0.00145 0.00940 0.00146 0.00259
## 5 0.00194 0.00409 -0.00430 0.00110
## 6 0.0214 0.0144 0.0109 0.0161
## 7 0.00437 0.00404 0.0126 0.00332
## 8 -0.0110 -0.00254 -0.00451 0.00305
## 9 -0.00342 0.0105 -0.00212 -0.00929
## 10 -0.00246 0.00219 0.00659 0.00202
## # ... with 999,990 more rows
Como já comentei outras vezes, o pacote ffp disponibiliza a família de funções view_on_* para construção de opiniões. Hoje utilizo view_on_marginal_distribution para impor views com base no painel recém gerado:
library(ffp)
prior_from_simulation <- rep(1 / 1000000, 1000000)
views <- view_on_marginal_distribution(
x = x,
simul = t_margins$marginal,
p = prior_from_simulation
)
views
## # ffp view
## Type: View On Marginal Distribution
## Aeq : Dim 16 x 1859
## beq : Dim 16 x 1
As listas Aeq e beq contidas no objeto views têm \(16\) linhas, ou seja, há \(16\) restrições ativas nessa opinião.
Por quê tantas restrições? Porque a função view_on_marginal_distribution foi desenhada para que a média, variância, assimetria e curtose sejam idênticas as do painel simulado, t_margins. Temos, portanto, \(4\) restrições ativas para cada ativo, totalizando \(16\) restrições.
Do ponto de vista matemático, o problema que queremos resolver é:
$$ min \sum_{i=1}^I x_i(ln(x_i) - ln(p_i)) $$
\(s.t.\)
$$ \sum_{i=1}^I \hat{p_i} O_{i,k} = \sum_{i=1}^I p_i \hat{O}_{i,k} $$ $$ \sum_{i=1}^I \hat{p_i} (O_{i,k})^2 = \sum_{i=1}^I p_i (\hat{O}_{i,k})^2 $$ $$ \sum_{i=1}^I \hat{p_i} (O_{i,k})^3 = \sum_{i=1}^I p_i (\hat{O}_{i,k})^3 $$
$$ \sum_{i=1}^I \hat{p_i} (O_{i,k})^4 = \sum_{i=1}^I p_i (\hat{O}_{i,k})^4 $$
Esse sistema é resolvido com a função entropy_pooling:
prior_from_data <- rep(1 / nrow(x), nrow(x))
ep <- entropy_pooling(
p = prior_from_data,
Aeq = views$Aeq,
beq = views$beq,
solver = "nlminb"
)
ep
## <ffp[1859]>
## 0.0005413464 0.0005623505 0.0005365219 0.0005426697 0.0005397119 ... 0.0005045393
O objeto ep contém as probabilidades que distorcem ao mínimo o vetor de probabilidades equal-weighted e que ao mesmo tempo atendem as restrições desejadas.
library(ggplot2)
autoplot(ep) +
scale_color_viridis_c(option = "C", end = 0.75) +
labs(title = "Distribuição de Probabilidades Posteriores",
subtitle = "Opinião nas Margens: distribuição t assimétrica",
x = NULL,
y = NULL)
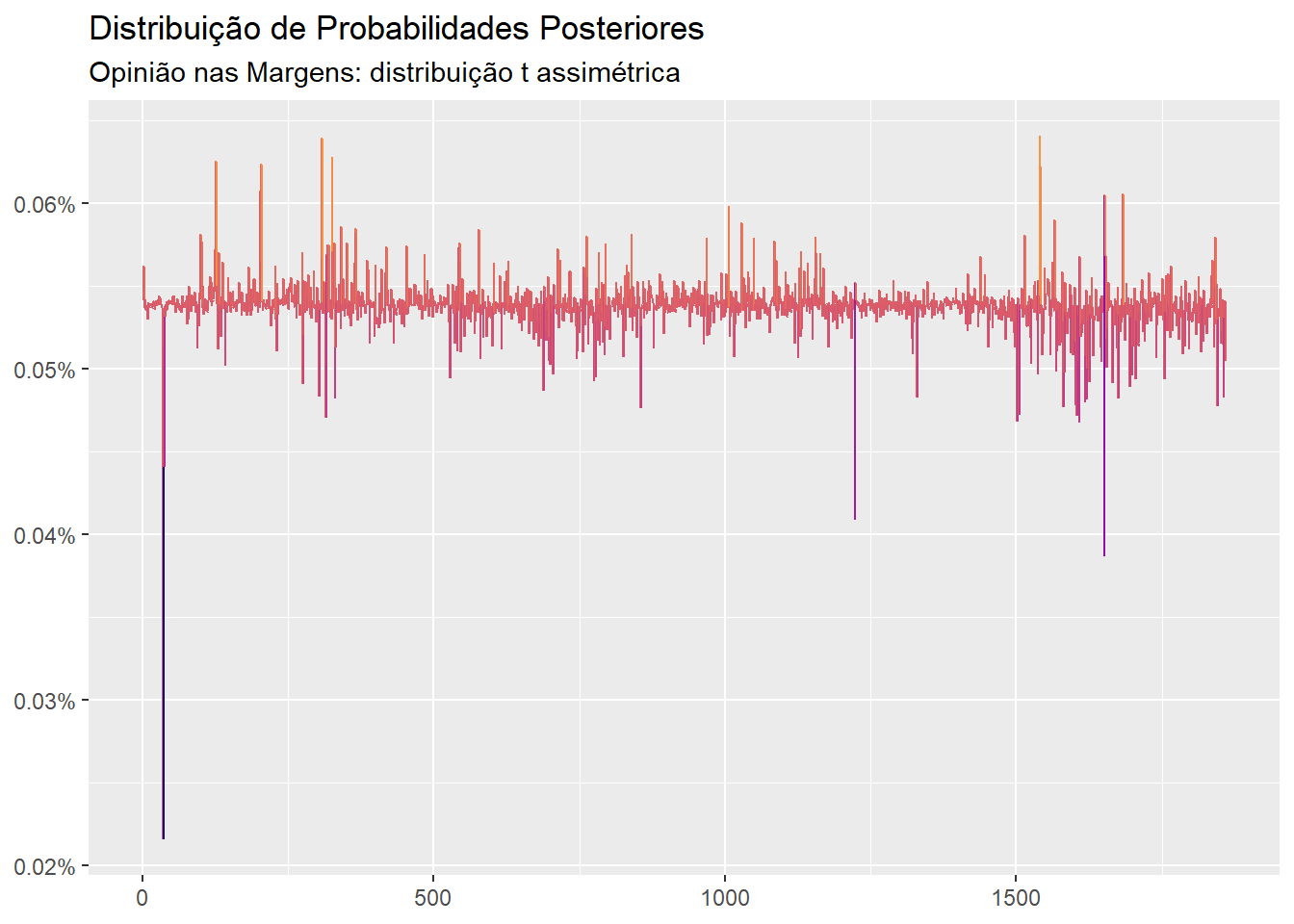
Com base nessas probabilidades é possível computar as estimativas de locação e dispersão condicionais:
cond_moments <- ffp_moments(x = x, p = ep)
cond_moments
## $mu
## DAX SMI CAC FTSE
## 0.0006447704 0.0008035049 0.0004324977 0.0004298670
##
## $sigma
## DAX SMI CAC FTSE
## DAX 1.004220e-04 6.217232e-05 8.018707e-05 5.065303e-05
## SMI 6.217232e-05 8.073073e-05 5.986606e-05 4.147749e-05
## CAC 8.018707e-05 5.986606e-05 1.215396e-04 5.655088e-05
## FTSE 5.065303e-05 4.147749e-05 5.655088e-05 6.343343e-05
Observe que o momentos condicionais batem exatamente com os momentos do painel simulado:
# Location Matches
round(cond_moments$mu / colMeans(t_margins$marginal) - 1, 2)
## DAX SMI CAC FTSE
## 0 0 0 0
# Dispersion Matches
round(sqrt(diag(cond_moments$sigma)) / apply(t_margins$marginal, 2, sd) - 1, 2)
## DAX SMI CAC FTSE
## 0 0 0 0
E divergem dos momentos incondicionais:
# Location doesn't match
round(cond_moments$mu / colMeans(x) - 1, 2)
## DAX SMI CAC FTSE
## -0.01 -0.02 -0.01 0.00
# Dispersion doesn't match
round(sqrt(diag(cond_moments$sigma)) / apply(x, 2, sd) - 1, 2)
## DAX SMI CAC FTSE
## -0.03 -0.03 0.00 0.00
Ou seja, a opinião dos econometristas é, de fato, levada em consideração no processo de otimização.
Agora vamos continuar com a brincadeira… Digamos que os analistas da gestora estejam pessimistas e acreditem que os retornos de todos os ativos terão um desempenho \(10\%\) abaixo da média histórica. Digamos também que os econometristas estejam preocupados com um possível aumento da volatilidade e achem prudente reduzir o número de graus de liberdade de \(\nu = 4.2\)2 para \(\nu = 2\):
# Return 10% below average
t_model$mu <- t_model$mu * 0.9
# degrees of freedom will be 2
t_model$chi <- 2.0
Para incorporar essas informações no modelo, as probabilidades precisam ser reestimadas:
new_margins <- generate_margins(model = t_model, n = 1000000)
views <- view_on_marginal_distribution(
x = x,
simul = new_margins$marginal,
p = prior_from_simulation
)
ep <- entropy_pooling(
p = prior_from_data,
Aeq = views$Aeq,
beq = views$beq,
solver = "nlminb"
)
cond_moments <- ffp_moments(x = x, p = ep)
E veja que mais uma vez as opiniões são satisfeitas:
# Location Matches
round(cond_moments$mu / colMeans(new_margins$marginal) - 1, 2)
## DAX SMI CAC FTSE
## 0 0 0 0
# Dispersion Matches
round(sqrt(diag(cond_moments$sigma)) / apply(new_margins$marginal, 2, sd) - 1, 2)
## DAX SMI CAC FTSE
## 0 0 0 0
Os momentos condicionais são a grande jóia da coroa das probabilidades flexíveis. Muitas vezes, uma diferença pequena entre as estimativas - condicionais vs incondicionais - pode ter um impacto enorme sobre a alocação final.
Contudo, as margens não são o único elemento em que podemos construir opiniões com ffp e cma. No próximo post falarei mais sobre uma fonte de associação “invisível”, mas extremamente relevante para modelagem de eventos de euforia e pânico.