Nem sempre os gestores possuem opiniões precisas sobre os parâmetros de locação e dispersão. Às vezes, as opiniões são mais sutis: a inclinação da curva de juros vai aumentar, o Ibovespa vai cair, o dólar vai ficar de lado, etc.

Para mostrar como entropy-pooling acomoda essas opiniões de posição (ou “rankiamento”) mais uma vez utilizo o dataset EuStockMarkets, que vem junto com a instalação do R:

x <- diff(log(EuStockMarkets))
head(x)

##               DAX          SMI          CAC         FTSE
## [1,] -0.009326550  0.006178360 -0.012658756  0.006770286
## [2,] -0.004422175 -0.005880448 -0.018740638 -0.004889587
## [3,]  0.009003794  0.003271184 -0.005779182  0.009027020
## [4,] -0.001778217  0.001483372  0.008743353  0.005771847
## [5,] -0.004676712 -0.008933417 -0.005120160 -0.007230164
## [6,]  0.012427042  0.006737244  0.011714353  0.008517217

Com base nesses dados, vamos supor que o time de gestão acredite que os retornos dos índices \(SMI\) e \(DAX\) estarão encadeados da seguinte maneira:

$$ SMI \leq DAX $$ Ou seja, o \(DAX\) performará melhor do que \(SMI\). Já em relação ao para o \(CAC\) e \(FTSE\), a postura é passiva e não há opinião formada.

Para montar esse tipo de opinião fraca, o pacote ffp disponibiliza a função view_on_rank:

library(ffp)

views <- view_on_rank(x = x, rank = c(2, 1))
views

## # ffp view
## Type:  View On Rank
## A :  Dim 1 x 1859 
## b :  Dim 1 x 1

No argumento rank devemos indicar o número da coluna de cada ativo em x, de maneira que aqueles com as melhores perspectivas de retorno estejam localizados à direita dos demais. Como achamos que o \(DAX\) (1 coluna) irá performar melhor do que o \(SMI\) (2 coluna) usamos rank = c(2, 1).

Matematicamente, estamos buscando minimizar a expressão:

$$ \sum_{i=1}^I x_i(ln(x_i) - ln(p_i)) $$ sujeito a restrição:

$$ p_i (SMI - DAX) \leq 0 $$ A função que soluciona esse problema é entropy_pooling:

prior <- rep(1 / nrow(x), nrow(x))
ep <- entropy_pooling(p = prior, A = views$A, b = views$b, solver = "nloptr")
ep

## <ffp[1859]>
## 0.0005145646 0.0005403155 0.0005470049 0.0005330238 0.0005446858 ... 0.0005469164

Note que pela primeira vez abandonamos o solver = "nlmimb", pois problemas com restrições de desigualdade devem ser resolvidos com os otimizadores solnl ou nloptr.

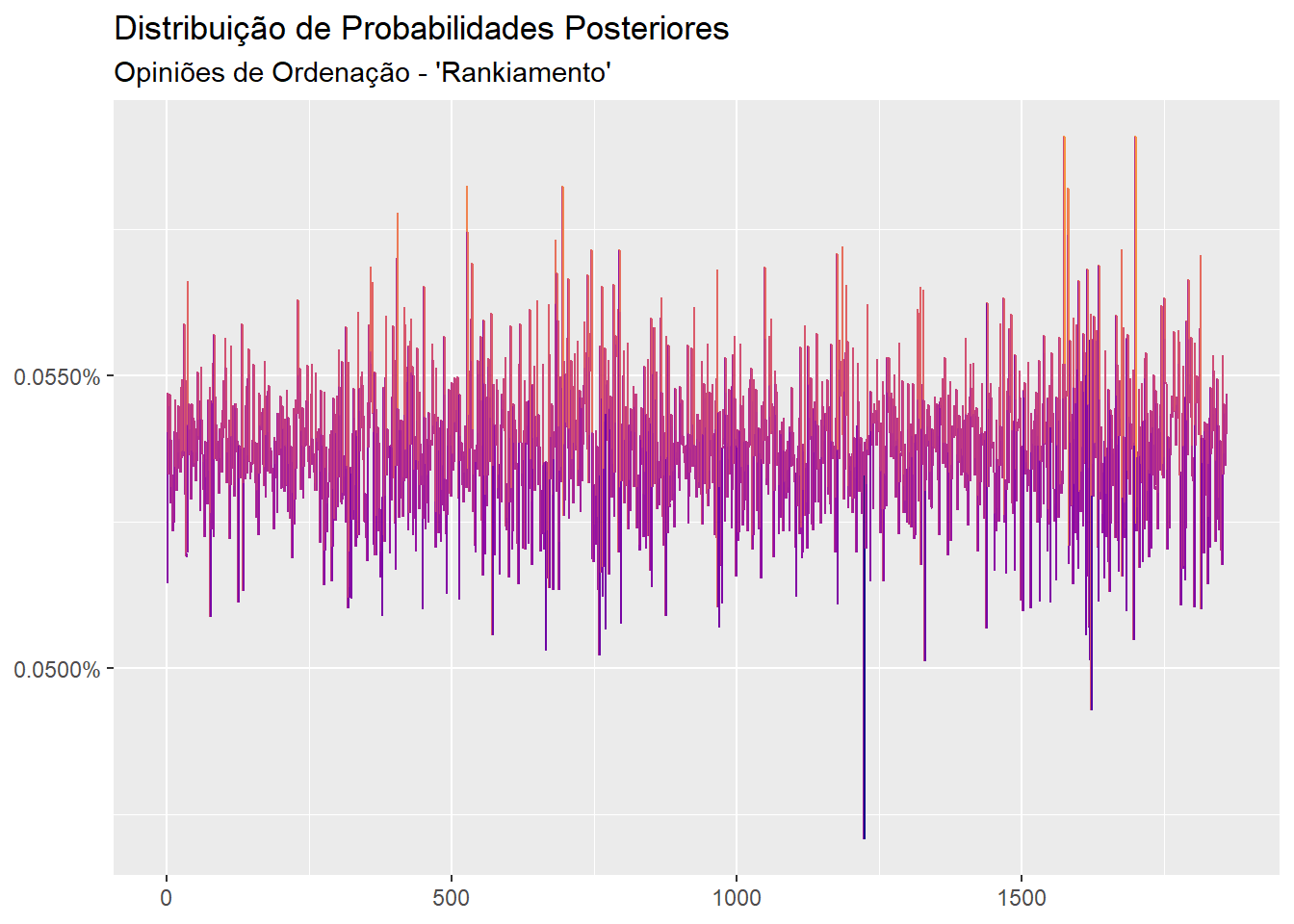
As probabilidades posteriores (que solucionam o problema da entropia mínima relativa) são visualizados com o método autoplot do pacote ggplot2:

library(ggplot2)

autoplot(ep) + 
  scale_color_viridis_c(option = "C", end = 0.75) + 
  labs(title    = "Distribuição de Probabilidades Posteriores", 
       subtitle = "Opiniões de Ordenação - 'Rankiamento'", 
       x        = NULL, 
       y        = NULL)

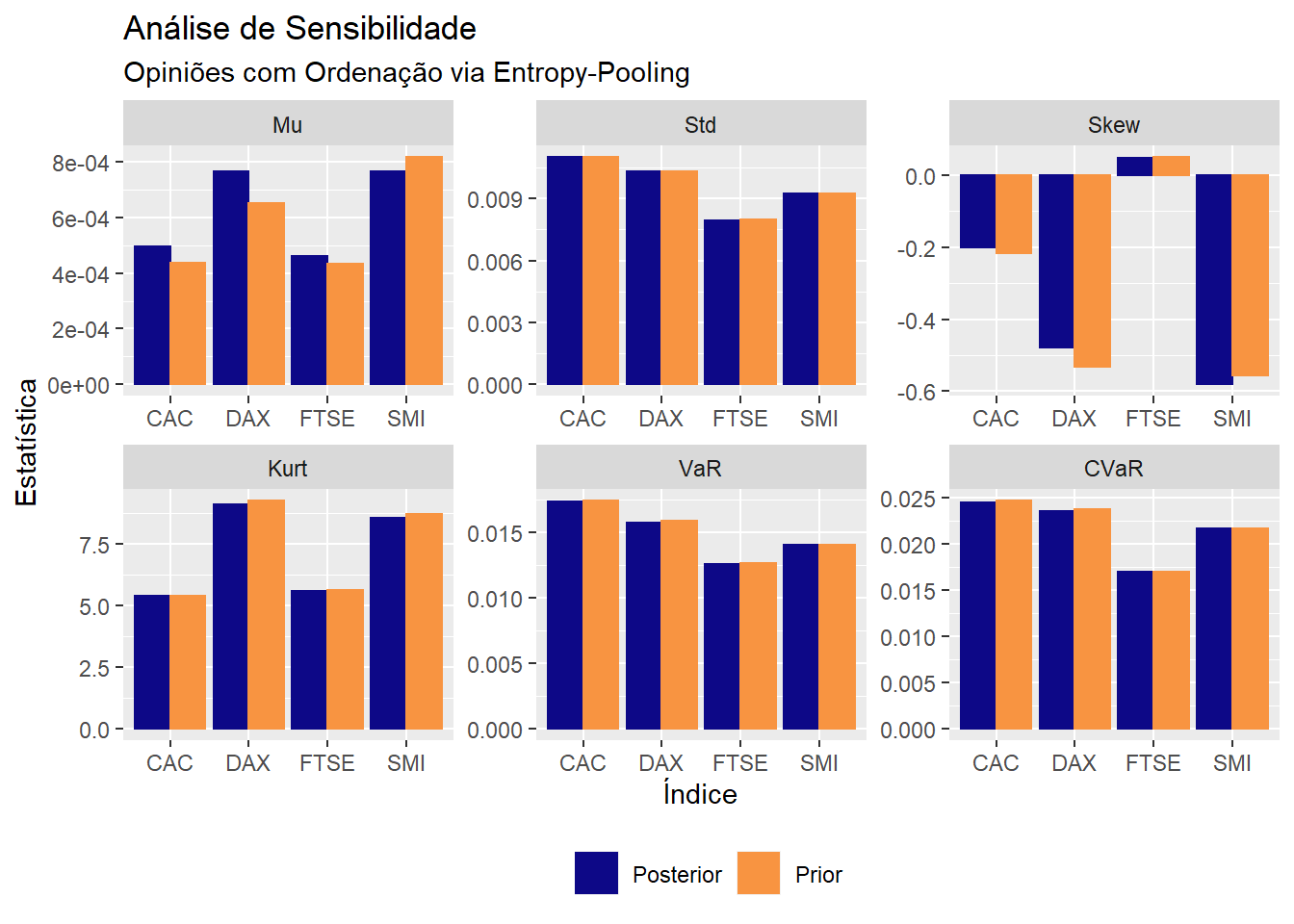
A razão entre os momentos - condicionais vs. incondicionais - de locação mostra que a restrição foi atendida: o retorno esperado do \(DAX\) aumentou em \(17\%\) (em relação a prior) e o retorno do índice \(SMI\) foi rebaixado em \(6,5\%\).

cond_moments <- ffp_moments(x = x, p = ep)

cond_moments$mu / colMeans(x) - 1

##         DAX         SMI         CAC        FTSE 
##  0.17274275 -0.06507207  0.13576463  0.06261163

Note que embora não fosse a intenção, os retornos projetados para os índices \(CAC\) e \(FTSE\) também foram alterados. Nesse caso, a função view_on_mean poderia ser utlizada para “redirecionar” a locação de volta para as médias amostrais, como mostra o post Opiniões nos retornos esperados.

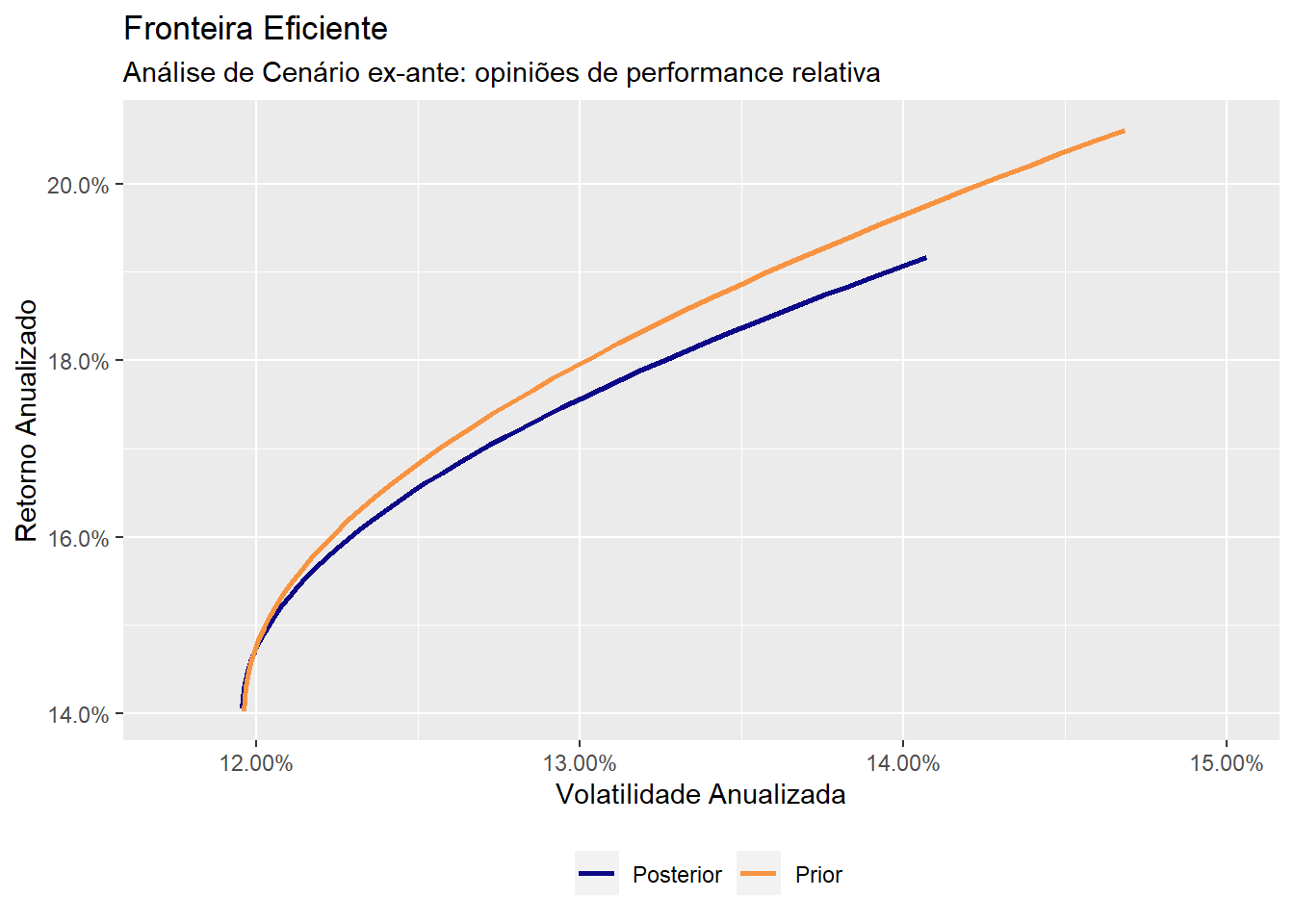
A fronteira eficiente condicional se situa abaixo da fronteira incondicional porque a opinião coloca um teto na performance do índice mais rentável - \(SMI \leq DAX\):

(1 + colMeans(x)) ^ 252 - 1

##       DAX       SMI       CAC      FTSE 
## 0.1785218 0.2287857 0.1164048 0.1149803

Como já mencionei outras vezes, é fácil estender esse tipo de análise para o VaR, Expected Shortfall, etc. De fato, ffp oferece um atalho para esses cálculos com empirical_stats:

library(dplyr)

prior_stats <- empirical_stats(x = x, p = as_ffp(prior), level = 0.05) |> 
  mutate(Regime = "Prior")
posterior_stats <- empirical_stats(x = x, p = ep, level = 0.05) |> 
  mutate(Regime = "Posterior")

# Plot
bind_rows(posterior_stats, prior_stats) |> 
  ggplot(aes(x = name, y = value, fill = Regime, color = Regime)) + 
  geom_col(position = "dodge") + 
  facet_wrap(~ stat, scales = "free") + 
  scale_fill_viridis_d(option = "C", end = 0.75) + 
  scale_color_viridis_d(option = "C", end = 0.75) + 
  theme(legend.position = "bottom") + 
  labs(title    = "Análise de Sensibilidade", 
       subtitle = "Opiniões com Ordenação via Entropy-Pooling", 
       x        = "Índice", 
       y        = "Estatística", 
       fill     = NULL,
       color    = NULL)