Hoje mostro como adicionar opiniões nas correlações dos ativos com ffp. Como de praxe, a análise é conduzida utilizando o dataset EuStockMarkets:

# invariance
x <- diff(log(EuStockMarkets))
cor(x)

##            DAX       SMI       CAC      FTSE
## DAX  1.0000000 0.7031219 0.7344304 0.6394674
## SMI  0.7031219 1.0000000 0.6160454 0.5847791
## CAC  0.7344304 0.6160454 1.0000000 0.6485679
## FTSE 0.6394674 0.5847791 0.6485679 1.0000000

Vamos assumir que o time de gestão acredite que a correlação entre os índices FTSE e DAX aumentará em \(30\%\) (de \(0.64\) para \(0.83\)) e gostaria de avaliar ex-ante o impacto dessa mudança sobre o ponto de ótimo.

Para imputar esse tipo de opinião o pacote ffp disponibiliza a função view_on_correlation:

library(ffp)

cor_opinion <- cor(x)
cor_opinion[4, 1] <- 0.83
cor_opinion[1, 4] <- 0.83

view_cor <- view_on_correlation(x = x, cor = cor_opinion)
view_cor

## # ffp view
## Type:  View On Correlation
## Aeq :  Dim 10 x 1859 
## beq :  Dim 10 x 1

No total, há 10 restrições em cada uma das matrizes Aeq e beq. Isso porque deseja-se alterar a correlação entre DAX e FTSE mantendo os demais elementos que não pertencem a diagonal principal intactos.

A minimização da distorção que acomoda essas opiniões é calculada com entropy_pooling:

prior <- rep(1 / nrow(x), nrow(x))
ep <- entropy_pooling(p = prior, Aeq = view_cor$Aeq, beq = view_cor$beq, solver = "nlminb")
ep

## <ffp[1859]>
## 6.709143e-05 0.000659403 0.001085763 0.0003254822 0.0005215729 ... 0.0004748052

O objeto ep é o vetor de probabilidades que soluciona o problema:

$$ min \sum_{i=1}^I x_i(ln(x_i) - ln(p_i)) $$ \(s.a.\) $$ \sum_{i=1}^I \hat{p_i} x_{j,k}x_{j,l} = \hat{m}_k \hat{m}_l + \hat{\sigma}_{k} \hat{\sigma}_{l} \hat{C}_{k, l} $$ Ou seja, dentre todos os possíveis vetores que atendem a restrição imposta, ep é aquele que distorce ao mínimo o vetor de probabilidades uniforme (equal-weighted).

Lembre-se que o método autoplot está disponível para objetos da classe ffp:

library(ggplot2)

autoplot(ep) + 
  scale_color_viridis_c(option = "C", end = 0.75) + 
  labs(title    = "Distribuição de Probabilidades Posteriores", 
       subtitle = "Opinião nas Correlações", 
       x        = NULL, 
       y        = NULL)

E que os momentos condicionais de locação e dispersão são acessados com ffp_moments:

cond_moments <- ffp_moments(x = x, p = ep)
cond_moments

## $mu
##          DAX          SMI          CAC         FTSE 
## 3.829225e-04 6.607859e-04 3.126221e-04 5.343587e-05 
## 
## $sigma
##               DAX          SMI          CAC         FTSE
## DAX  1.057151e-04 6.616018e-05 8.319569e-05 6.834306e-05
## SMI  6.616018e-05 8.614758e-05 6.424798e-05 4.518376e-05
## CAC  8.319569e-05 6.424798e-05 1.222682e-04 5.754929e-05
## FTSE 6.834306e-05 4.518376e-05 5.754929e-05 6.341578e-05

Observe que a estrutura de correlação posterior se aproxima do cenário esperado, \(cor(DAX, FTSE) = 0.83\):

cov2cor(cond_moments$sigma)

##            DAX       SMI       CAC      FTSE
## DAX  1.0000000 0.6932767 0.7317714 0.8346939
## SMI  0.6932767 1.0000000 0.6260098 0.6113109
## CAC  0.7317714 0.6260098 1.0000000 0.6535585
## FTSE 0.8346939 0.6113109 0.6535585 1.0000000

Violá!

Obviamente, a função view_on_correlation poderia ser utilizada também para stress-testing. Por exemplo, digamos que a gestora acredite que o mercado entrará em modo de “pânico” com as correlações subindo uniformemente para \(0.9\):

co <- matrix(0.9, 4, 4)
diag(co) <- 1
co

##      [,1] [,2] [,3] [,4]
## [1,]  1.0  0.9  0.9  0.9
## [2,]  0.9  1.0  0.9  0.9
## [3,]  0.9  0.9  1.0  0.9
## [4,]  0.9  0.9  0.9  1.0

Repetindo o mesmo processo obtem-se um novo vetor de probabilidades que satisfaz o cenário de “pânico”:

view_panic <- view_on_correlation(x = x, cor = co)

ep_panic <- entropy_pooling(
  p      = prior, 
  Aeq    = view_panic$Aeq, 
  beq    = view_panic$beq, 
  solver = "nlminb"
)

autoplot(ep_panic) +
  scale_color_viridis_c(option = "C", end = 0.75) + 
  labs(title    = "Distribuição de Probabilidades Posteriores", 
       subtitle = "Opinião nas Correlações: cenário de pânico", 
       x        = NULL, 
       y        = NULL)

E que ao mesmo tempo atende as restrições desejadas:

cov2cor(ffp_moments(x = x, p = ep_panic)$sigma)

##            DAX       SMI       CAC      FTSE
## DAX  1.0000000 0.9039114 0.9079263 0.8980729
## SMI  0.9039114 1.0000000 0.9057270 0.8878958
## CAC  0.9079263 0.9057270 1.0000000 0.8934409
## FTSE 0.8980729 0.8878958 0.8934409 1.0000000

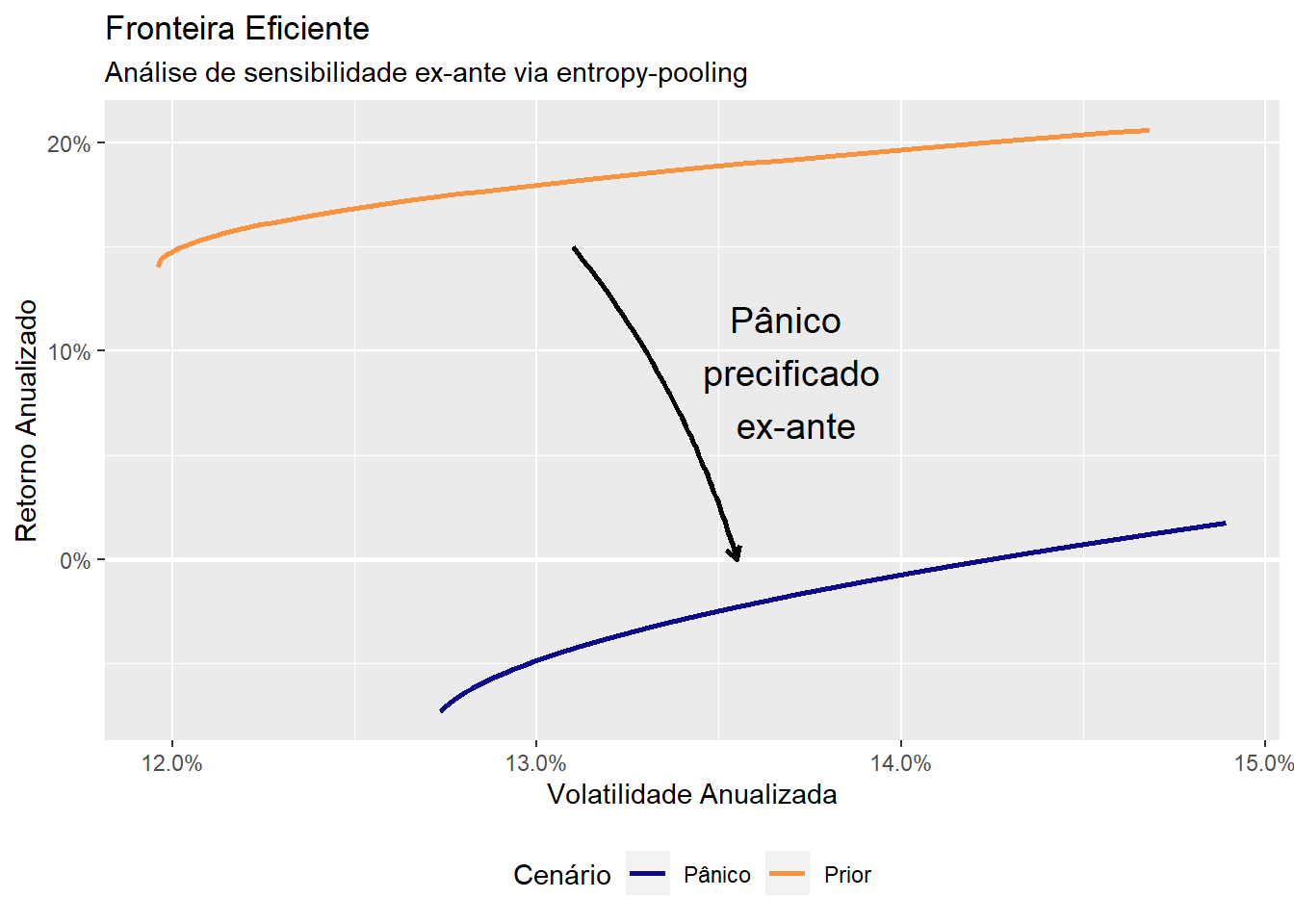
A possibilidade de se precificar rapidamente qualquer opinião é uma das grandes virtudes de entropy-pooling.

Por hoje é isso. No próximo post mostro como construir opiniões que devem ser satisfeitas com desigualdade.