Dando sequência aos posts anteriores, hoje mostro como adicionar opiniões nas volatilidades esperadas.

Continuo utilizando o dataset EuStockMarkets (que acompanha o R) para facilitar a replicação dos códigos utilizados:

x <- diff(log(EuStockMarkets))
head(x)

##               DAX          SMI          CAC         FTSE
## [1,] -0.009326550  0.006178360 -0.012658756  0.006770286
## [2,] -0.004422175 -0.005880448 -0.018740638 -0.004889587
## [3,]  0.009003794  0.003271184 -0.005779182  0.009027020
## [4,] -0.001778217  0.001483372  0.008743353  0.005771847
## [5,] -0.004676712 -0.008933417 -0.005120160 -0.007230164
## [6,]  0.012427042  0.006737244  0.011714353  0.008517217

Vamos assumir que um dos modelos proprietários do time de gestão aponte para os seguintes retornos esperados: DAX, \(+15\%\); SMI, \(+10\%\); CAC, \(+10\%\) e FTSE, \(+5\%\).

A gestora gostaria de construir um portfolio que leve em conta essas informações - subjetivas - mas sem deixar de lado o controle de risco, em particular, da volatilidade. Nesse caso, assumo que a gestora deseje utilizar a volatilidade um portfolio equal-weighted como referência:

ref_vol_model <- x %*% rep(0.25, 4)
vol_model <- stats::sd(ref_vol_model) * sqrt(252) 

paste0(round(100 * vol_model, 2), "%")

## [1] "13.21%"

Ou seja, um dos objetivos é “ancorar” a volatilidade em torno de \(13\%\) ao ano.

Para incorporar essas visões de mundo, é necessário criar opiniões nos retornos esperados e nas volatilidades. Esse processo é realizado com a família de funções view_on_*() que fazem parte do pacote ffp:

library(ffp)

# Subjective Valuation
valuation <- {(1 + c(0.15, 0.1, 0.1, 0.05)) ^ (1 / 252)} - 1

# Views Constructor
view_return     <- view_on_mean(x = x, mean = valuation)
view_volatility <- view_on_volatility(x = ref_vol_model, vol = stats::sd(ref_vol_model))

Para combinar múltiplas opiniões, o pacote ffp disponibiliza a função bind_views:

views <- bind_views(view_return, view_volatility)
views

## # ffp view
## Type:  Multiple Views
## Aeq :  Dim 5 x 1859 
## beq :  Dim 5 x 1 
## A :  Dim 0 x 1 
## b :  Dim 0 x 1

Lembre-se que em entropy-pooling, cada opinião entra como uma restrição linear no problema da Entropia Mínima Relativa (EMR). Em nosso caso, temos \(4\) opiniões para os retornos esperados e \(1\) opinião para volatilidade. Assim, as matrizes Aeq e beq contêm \(5\) linhas cada, uma para cada restrição.

O vetor de probabilidades ótimo - \(p^*\) - que cria a menor distorção possível em relação as probabilidades equal-weighted (uma prior que emerge naturalmente) é calculado com a função entropy_pooling:

prior <- rep(1 / nrow(x), nrow(x))
ep <- entropy_pooling(p = prior, Aeq = views$Aeq, beq = views$beq, solver = "nlminb")

O método autoplot está disponível para visualização de objetos da classe ffp:

library(ggplot2)

autoplot(ep) + 
  scale_color_viridis_c(option = "C", end = 0.75) + 
  labs(title    = "Distribuição de Probabilidades Posteriores", 
       subtitle = "Opiniões na Volatilidade e Retornos Esperados", 
       x        = NULL, 
       y        = NULL)

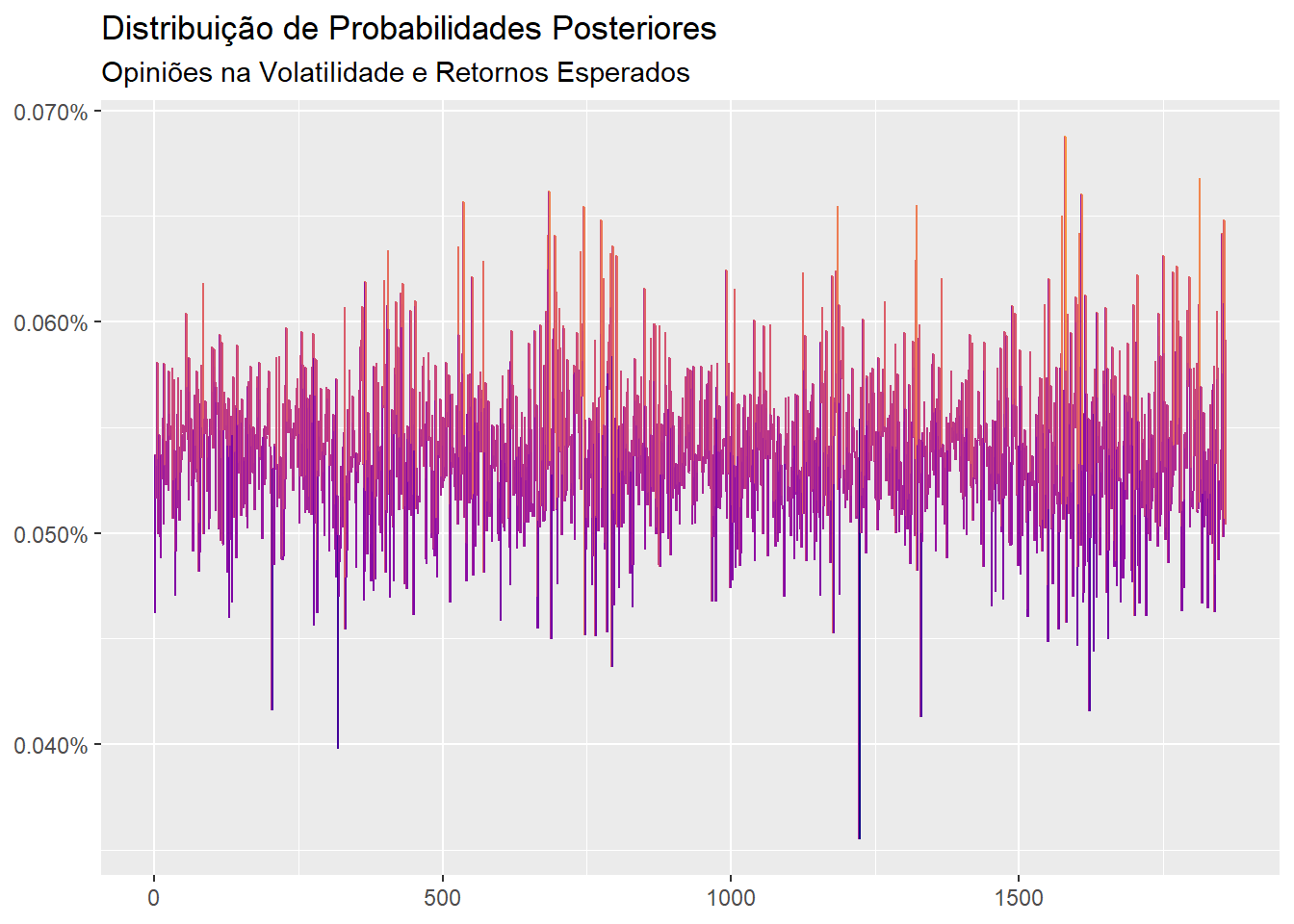
Os momentos condicionais - que acomodam as visões da gestora - são calculados com ffp_moments:

cond_moments <- ffp_moments(x = x, p = ep)
cond_moments

## $mu
##          DAX          SMI          CAC         FTSE 
## 0.0005547647 0.0003782865 0.0003782865 0.0001936305 
## 
## $sigma
##               DAX          SMI          CAC         FTSE
## DAX  1.063495e-04 6.746852e-05 8.355328e-05 5.284606e-05
## SMI  6.746852e-05 8.595718e-05 6.308962e-05 4.343771e-05
## CAC  8.355328e-05 6.308962e-05 1.214515e-04 5.720668e-05
## FTSE 5.284606e-05 4.343771e-05 5.720668e-05 6.292183e-05

Um teste rápido mostra que as opiniões para os retornos esperados foram respeitados durante o processo de otimização:

(1 + cond_moments$mu) ^ 252 - 1

##  DAX  SMI  CAC FTSE 
## 0.15 0.10 0.10 0.05

Assim como as expectativas em relação a volatilidade:

vol_results <- c(stats::sd(ref_vol_model), sqrt(ffp_moments(x = ref_vol_model, ep)$sigma))
names(vol_results) <- c("Prior", "Posterior")
vol_results * sqrt(252)

##     Prior Posterior 
## 0.1321068 0.1323336

Obviamente, a gestora poderia utilizar outros modelos para estimar a volatilidade, ao invés de stats::sd: GARCH, TVPVAR, FAVAR, etc. seriam igualmente válidos e provavelmente se sairíam melhores out-of-sample.

Uma vez que os momentos condicionais tenham sido computados, o impacto ex-ante das opiniões no ponto de ótimo é estimado num piscar de olhos via programação quadrática e/ou cônica.

Chegaremos lá…