Quanto encolhimento o mercado de ações requer?

Bernardo Reckziegel 2021-12-06 11 min read

In 1956 Charles Stein mostrou um resultado incrível: para dados multivariados a média amostral não é um estimador ótimo de localização¹. Há uma maneira de aprimorar a estimativa final por meio do trade-off entre viés e variância.

Esse aprimoramento pode ser realizado pelo que chamamos de “encolhimento” (shrinkage).

“Encolhimento” nada mais é do que uma média ponderada entre diferente estimadores. Geralmente, é composto de três partes:

Um estimador com pouca ou quase nenhuma estrutura (não-paramétrico);
Um estimador com muita estrutura (paramétrico); e
Uma constante de intensidade entre $0$ e $1$ que determinará quanto peso será dado para os estimadores com e sem estrutura.

Jorrion (1986) foi o primeiro a aplicar esse conceito para otimização de carterias. Quase $20$ anos depois, Ledoit&Wolf (LW) publicaram Honey, I Shrunk the Sample Covariance Matrix, que se tornou um clássico da literatura.

Nesse post, implemento a equação (2) que aparece em LW:

$$ \hat{\Sigma}_{Shrink} = \hat{\delta} F + (1 - \hat{\delta}) S $$

O principal objetivo é estimar $\hat{\delta^*}$ , o nível de encolhimento ótimo para o índice Dow Jones usando uma base de dados diária.

Também analiso se $\hat{\delta^*}$ é constante ao longo do tempo e se o erro de estimação implícito por esse modelo vem aumentando ou diminuindo.

Vamos começar!

# Bibliotecas requeridas
library(tidyverse)
library(rsample)
library(YahooTickers)

Para baixar os dados do índice Dow Jones utilizo o pacote YahooTickers, que foi criado por mim. Você encontra informações sobre essa biblioteca nesse post ou no github: https://reckziegel.github.io/YahooTickers/.

ticks  <- get_tickers(dow)
stocks <- get_stocks(tickers = ticks, from = "2000-01-01")
stocks

## # A tibble: 157,673 x 8
##    date       tickers  open  high   low close  volume adjusted
##    <date>     <fct>   <dbl> <dbl> <dbl> <dbl>   <dbl>    <dbl>
##  1 2000-01-03 MMM      48.0  48.2  47.0  47.2 2173400     27.0
##  2 2000-01-04 MMM      46.4  47.4  45.3  45.3 2713800     25.9
##  3 2000-01-05 MMM      45.6  48.1  45.6  46.6 3699400     26.6
##  4 2000-01-06 MMM      47.2  51.2  47.2  50.4 5975800     28.8
##  5 2000-01-07 MMM      50.6  51.9  50.0  51.4 4101200     29.4
##  6 2000-01-10 MMM      50.2  51.8  50    51.1 3863800     29.2
##  7 2000-01-11 MMM      50.4  51.2  50.2  50.2 2357600     28.7
##  8 2000-01-12 MMM      51.0  51.8  50.4  50.4 2868400     28.8
##  9 2000-01-13 MMM      50.7  50.9  50.2  50.4 2244400     28.8
## 10 2000-01-14 MMM      50.4  50.5  49.5  49.7 2541800     28.4
## # ... with 157,663 more rows

O objeto stocks contém dados financeiros desde o início do ano 2000. Contudo, nem todas as empresas do índice negociavam nessa data:

stocks |>
  group_by(tickers) |>
  summarise(n = n(), first_trading_date = min(date)) |>
  arrange(desc(first_trading_date))

## # A tibble: 30 x 3
##    tickers     n first_trading_date
##    <fct>   <int> <date>            
##  1 DOW       691 2019-03-20        
##  2 V        3460 2008-03-19        
##  3 CRM      4401 2004-06-23        
##  4 MMM      5523 2000-01-03        
##  5 AXP      5523 2000-01-03        
##  6 AMGN     5523 2000-01-03        
##  7 AAPL     5523 2000-01-03        
##  8 BA       5523 2000-01-03        
##  9 CAT      5523 2000-01-03        
## 10 CVX      5523 2000-01-03        
## # ... with 20 more rows

Para evitar trabalhar com dados desbalanceados filtro apenas as empresas que possuem mais de $3780$ dias de negociação (aproximadamente $15$ anos):

stocks_filtered <- stocks |>

  group_by(tickers) |>
  mutate(n = n()) |>
  filter(n > 3780) |>
  select(-n) |>
  ungroup() |>

  drop_na()

stocks_filtered

## # A tibble: 153,522 x 8
##    date       tickers  open  high   low close  volume adjusted
##    <date>     <fct>   <dbl> <dbl> <dbl> <dbl>   <dbl>    <dbl>
##  1 2000-01-03 MMM      48.0  48.2  47.0  47.2 2173400     27.0
##  2 2000-01-04 MMM      46.4  47.4  45.3  45.3 2713800     25.9
##  3 2000-01-05 MMM      45.6  48.1  45.6  46.6 3699400     26.6
##  4 2000-01-06 MMM      47.2  51.2  47.2  50.4 5975800     28.8
##  5 2000-01-07 MMM      50.6  51.9  50.0  51.4 4101200     29.4
##  6 2000-01-10 MMM      50.2  51.8  50    51.1 3863800     29.2
##  7 2000-01-11 MMM      50.4  51.2  50.2  50.2 2357600     28.7
##  8 2000-01-12 MMM      51.0  51.8  50.4  50.4 2868400     28.8
##  9 2000-01-13 MMM      50.7  50.9  50.2  50.4 2244400     28.8
## 10 2000-01-14 MMM      50.4  50.5  49.5  49.7 2541800     28.4
## # ... with 153,512 more rows

Por fim, calculo os retornos lineares e transformo os dados do formato tidy (longo) para o formato tabular (matricial):

stocks_wide <- stocks_filtered |>

  group_by(tickers) |>
  mutate(returns = adjusted / lag(adjusted) - 1) |>
  select(date, tickers, returns) |>
  ungroup() |>

  pivot_wider(names_from = tickers, values_from = returns) |>
  drop_na()

stocks_wide

## # A tibble: 4,400 x 29
##    date             MMM       AXP     AMGN      AAPL       BA       CAT      CVX
##    <date>         <dbl>     <dbl>    <dbl>     <dbl>    <dbl>     <dbl>    <dbl>
##  1 2004-06-24 -0.0108   -0.00837   0.00553 -0.0154   -0.00632  0.0155   -5.06e-3
##  2 2004-06-25  0.000904  0.00765  -0.00715  0.0157    0.0189  -0.0120   -1.07e-2
##  3 2004-06-28  0.000338 -0.00798  -0.0105  -0.0359   -0.0212  -0.00857  -6.10e-3
##  4 2004-06-29  0.0125    0.00648   0.00990  0.000308  0.00597  0.0173    6.68e-3
##  5 2004-06-30  0.00234   0.00410   0.00887  0.00123   0.0115   0.00787   7.17e-3
##  6 2004-07-01 -0.0204   -0.000973  0.00348 -0.00737  -0.0233  -0.0159   -6.80e-3
##  7 2004-07-02 -0.00760  -0.00175   0.00803 -0.0378   -0.00762 -0.0187   -2.35e-3
##  8 2004-07-06  0.000572 -0.00800  -0.0212  -0.00418  -0.00424  0.000131  1.50e-3
##  9 2004-07-07  0.0101    0.00354  -0.00259 -0.0181    0.00162  0.0100    5.35e-4
## 10 2004-07-08 -0.00780  -0.0145   -0.0106  -0.00823   0.0117  -0.0125   -9.63e-4
## # ... with 4,390 more rows, and 21 more variables: CSCO <dbl>, KO <dbl>,
## #   GS <dbl>, HD <dbl>, HON <dbl>, IBM <dbl>, INTC <dbl>, JNJ <dbl>, JPM <dbl>,
## #   MCD <dbl>, MRK <dbl>, MSFT <dbl>, NKE <dbl>, PG <dbl>, CRM <dbl>,
## #   TRV <dbl>, UNH <dbl>, VZ <dbl>, WBA <dbl>, WMT <dbl>, DIS <dbl>

A Matrix de Covariância

Em seu site pessoal, Michael Wolf disponibiliza em MATLAB o código de diversas publicações. Tomei a liberdade de traduzir a função utlizada no paper Honey, I Shrunk the Sample Covariance Matrix para o R².

Fica assim:

honey_shrunk <- function(R, shrink = NULL) {
    # "Honey, I Shrunk the Sample Covariance Matrix"
    # http://www.ledoit.net/honey.pdf
    # https://www.econ.uzh.ch/en/people/faculty/wolf/publications.html
    n  <- nrow(R)
    p  <- ncol(R)
    mu <- apply(R, 2, mean)
    R  <- R - matrix(rep(mu, times = n), ncol = p, byrow = TRUE)
    
    # Covariancia amostral usando  (R - mean)
    sample  <- (1 / n) * (t(R) %*% R)
    # Prior
    var     <- matrix(diag(sample), ncol = 1)
    sqrtvar <- sqrt(var)
    tmpMat  <- matrix(rep(sqrtvar, times = p), nrow = p)
    rBar    <- (sum(sum(sample / (tmpMat * t(tmpMat)))) - p) / (p * (p - 1))
    prior   <- rBar * tmpMat * t(tmpMat)
    diag(prior) <- var
    
    if (is.null(shrink)) {
        # pi-hat
        y      <- R ^ 2
        phiMat <- t(y) %*% y / n - 2 * (t(R) %*% R) * sample / n + sample ^ 2
        phi    <- sum(phiMat)
        # rho-hat
        aux1     <- (t(R ^ 3) %*% R) / n
        help     <- t(R) %*% R / n
        helpDiag <- matrix(diag(help), ncol = 1)
        aux2     <- matrix(rep(helpDiag, times = p), ncol = p) * sample
        aux3     <- help * matrix(rep(var, times = p), ncol = p)
        aux4     <- matrix(rep(var, times = p), ncol = p) * sample
        thetaMat <- aux1 - aux2 - aux3 + aux4
        diag(thetaMat) <- 0
        rho      <- sum(diag(phiMat)) + rBar * sum(sum(((1 / sqrtvar) %*% t(sqrtvar)) * thetaMat))
        # gamma-hat
        gamma <- norm(sample - prior, "F") ^ 2
        # Shrinkage constant
        kappa     <- (phi - rho) / gamma
        shrinkage <- max(0, min(1, kappa / n))
        
    } else {
      
        shrinkage <- shrink
        
    }
    
    # Estimador
    sigma <- shrinkage * prior + (1 - shrinkage) * sample
    out   <- list(cov = sigma, prior = prior, shrinkage = shrinkage)
    
    out
    
}

O output dessa função é uma lista com os seguintes objetos:

cov: é equivalente a $ \hat{\Sigma}_{Shrink} $ da equação (2);
prior: a matrix $ F $ que aparece na equação (3) do apêndice A; e
shrinkage: nível ótimo para o parâmetro $ \hat{\delta} $ que aparece na equação (2).

Janela de Estimação

Para responder a questão inicial - “Quanto encolhimento o mercado de ações requer?” - utilizo a função honey_shrunk() repetidamente em uma janela de tempo móvel (rolling window).

Para manter a estrutura simples, a estimação ocorre em janelas de 3 meses, 1 ano, 3 anos e 5 anos:

roll_tbl <- tibble(
  windows = c(90, 252, 252 * 3, 252 * 5),
  stocks  = list(stocks_wide),
  roll    = map2(
    .x = windows,
    .y = stocks,
    .f = ~ rolling_origin(data = .y, initial = .x, cumulative = FALSE)
    )
  ) |>
  unnest(cols = roll) |>
  mutate(.analysis = map(.x = splits, .f = analysis))
roll_tbl

## # A tibble: 15,242 x 5
##    windows stocks                splits         id        .analysis         
##      <dbl> <list>                <list>         <chr>     <list>            
##  1      90 <tibble [4,400 x 29]> <split [90/1]> Slice0001 <tibble [90 x 29]>
##  2      90 <tibble [4,400 x 29]> <split [90/1]> Slice0002 <tibble [90 x 29]>
##  3      90 <tibble [4,400 x 29]> <split [90/1]> Slice0003 <tibble [90 x 29]>
##  4      90 <tibble [4,400 x 29]> <split [90/1]> Slice0004 <tibble [90 x 29]>
##  5      90 <tibble [4,400 x 29]> <split [90/1]> Slice0005 <tibble [90 x 29]>
##  6      90 <tibble [4,400 x 29]> <split [90/1]> Slice0006 <tibble [90 x 29]>
##  7      90 <tibble [4,400 x 29]> <split [90/1]> Slice0007 <tibble [90 x 29]>
##  8      90 <tibble [4,400 x 29]> <split [90/1]> Slice0008 <tibble [90 x 29]>
##  9      90 <tibble [4,400 x 29]> <split [90/1]> Slice0009 <tibble [90 x 29]>
## 10      90 <tibble [4,400 x 29]> <split [90/1]> Slice0010 <tibble [90 x 29]>
## # ... with 15,232 more rows

Adicionando uma nova coluna com as datas para essa mesma tibble³:

get_assessment_date <- function(x) {
  purrr::map(.x = x$splits, .f = ~ rsample::assessment(.x)) |>
    purrr::map(~ timetk::tk_tbl(data = ., rename_index = "date", silent = TRUE)) |>
    purrr::map(.f = purrr::keep, .p = lubridate::is.Date) |>
    purrr::reduce(dplyr::bind_rows) |>
    dplyr::pull(date)
}

roll_tbl <- roll_tbl |>
  mutate(date = get_assessment_date(roll_tbl))
roll_tbl

## # A tibble: 15,242 x 6
##    windows stocks                splits         id        .analysis   date      
##      <dbl> <list>                <list>         <chr>     <list>      <date>    
##  1      90 <tibble [4,400 x 29]> <split [90/1]> Slice0001 <tibble [9~ 2004-11-01
##  2      90 <tibble [4,400 x 29]> <split [90/1]> Slice0002 <tibble [9~ 2004-11-02
##  3      90 <tibble [4,400 x 29]> <split [90/1]> Slice0003 <tibble [9~ 2004-11-03
##  4      90 <tibble [4,400 x 29]> <split [90/1]> Slice0004 <tibble [9~ 2004-11-04
##  5      90 <tibble [4,400 x 29]> <split [90/1]> Slice0005 <tibble [9~ 2004-11-05
##  6      90 <tibble [4,400 x 29]> <split [90/1]> Slice0006 <tibble [9~ 2004-11-08
##  7      90 <tibble [4,400 x 29]> <split [90/1]> Slice0007 <tibble [9~ 2004-11-09
##  8      90 <tibble [4,400 x 29]> <split [90/1]> Slice0008 <tibble [9~ 2004-11-10
##  9      90 <tibble [4,400 x 29]> <split [90/1]> Slice0009 <tibble [9~ 2004-11-11
## 10      90 <tibble [4,400 x 29]> <split [90/1]> Slice0010 <tibble [9~ 2004-11-12
## # ... with 15,232 more rows

O objeto roll_tbl se encontra no formato tidy e com isso fica fácil estimar o nível de encolhimento ótimo usando a família de funções map_* do pacote purrr:

intensity_fit <- roll_tbl |>
  mutate(intensity = map_dbl(
    .x = .analysis,
    .f = ~ honey_shrunk(as.matrix(.x[ , -1]))$shrinkage
    # -1 para descartar a coluna com as datas que é usada apenas para os gráficos.
    )
  )
intensity_fit

## # A tibble: 15,242 x 7
##    windows stocks                splits   id     .analysis  date       intensity
##      <dbl> <list>                <list>   <chr>  <list>     <date>         <dbl>
##  1      90 <tibble [4,400 x 29]> <split ~ Slice~ <tibble [~ 2004-11-01     0.365
##  2      90 <tibble [4,400 x 29]> <split ~ Slice~ <tibble [~ 2004-11-02     0.342
##  3      90 <tibble [4,400 x 29]> <split ~ Slice~ <tibble [~ 2004-11-03     0.330
##  4      90 <tibble [4,400 x 29]> <split ~ Slice~ <tibble [~ 2004-11-04     0.326
##  5      90 <tibble [4,400 x 29]> <split ~ Slice~ <tibble [~ 2004-11-05     0.303
##  6      90 <tibble [4,400 x 29]> <split ~ Slice~ <tibble [~ 2004-11-08     0.296
##  7      90 <tibble [4,400 x 29]> <split ~ Slice~ <tibble [~ 2004-11-09     0.302
##  8      90 <tibble [4,400 x 29]> <split ~ Slice~ <tibble [~ 2004-11-10     0.314
##  9      90 <tibble [4,400 x 29]> <split ~ Slice~ <tibble [~ 2004-11-11     0.320
## 10      90 <tibble [4,400 x 29]> <split ~ Slice~ <tibble [~ 2004-11-12     0.312
## # ... with 15,232 more rows

Visualização

Como esperado, o aumento do número de realizações diminui a necessidade de encolhimento:

intensity_fit |>
  mutate(windows = as_factor(windows)) |>
  ggplot(aes(x = date, y = intensity, color = windows)) +
  geom_line() +
  facet_wrap(~windows) + 
  labs(
    title    = "Intensidade de Encolhimento Requerida para Diferentes Janelas Temporais", 
    subtitle = "Ações do Índice Dow Jones - 2000-2021 - estimação em janelas móveis", 
    caption  = "Fonte: Yahoo Finance / Pacote `YahooTickers`"
    )

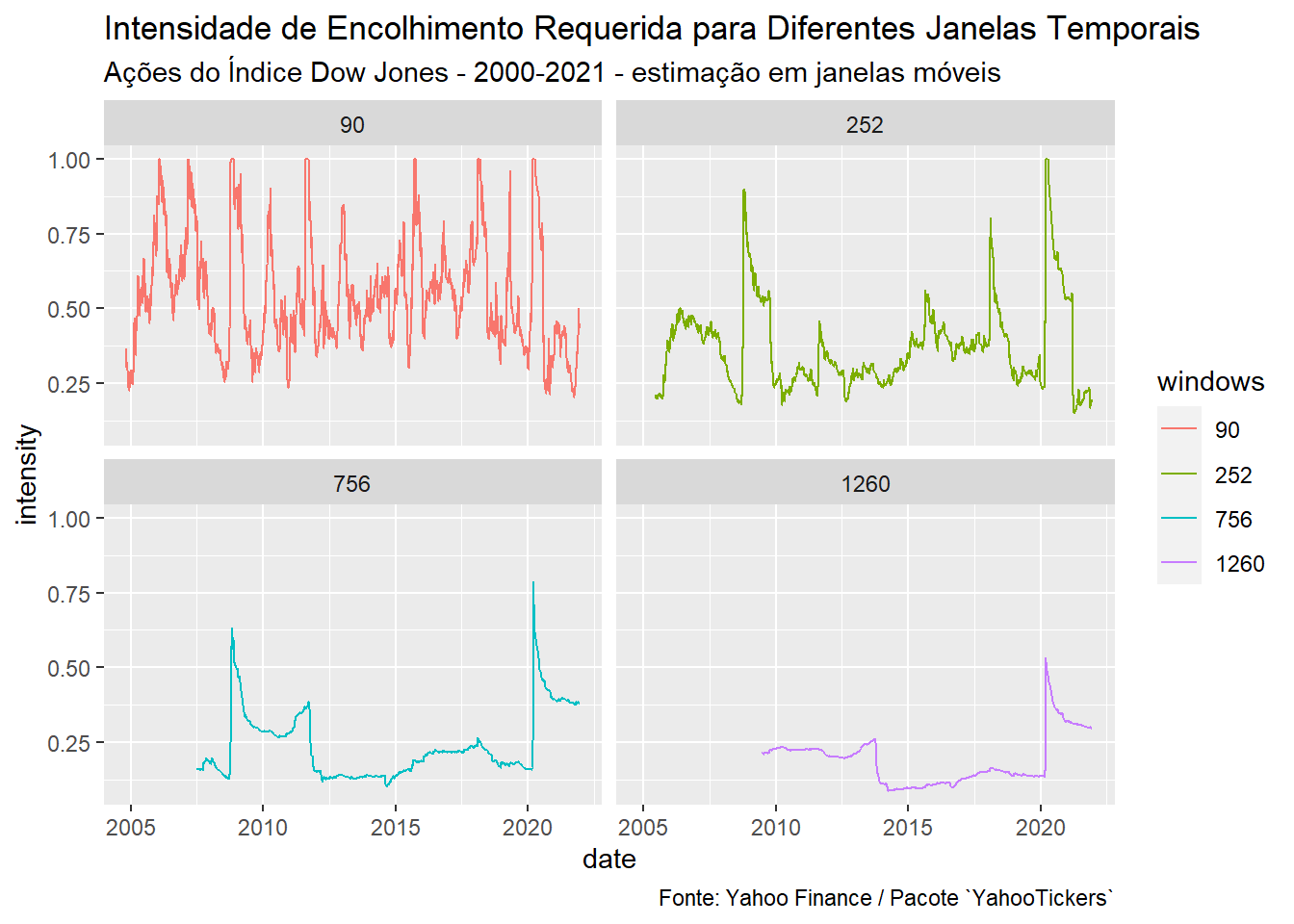
O nível de shrinkage aumenta significativamente após períodos de crises (2008 e 2020). Quando o pânico se instaura, as correlações quebram e a qualidade da informação embutida nos retornos históricos diminui. Nesses momentos, justifica-se a adoção de um estimador estruturado.

Em relação a evolução dessa estimativa, não parece haver uma tendência nítida de alta (ou baixa), exceto os saltos causados por eventos de pânico.

Por fim, é possível interpretar a razão entre $\delta$ e $1 - \delta$ como uma taxa de troca (taxa marginal de substituição) entre erro de estimação vs. erro de especificação existentes no mercado:

intensity_fit |>
  mutate(
    windows      = as_factor(windows), 
    error_amount = intensity / (1 - intensity)
    ) |> 
  ggplot(aes(x = date, y = error_amount, color = windows)) +
  geom_line() +
  coord_cartesian(ylim = c(0, 10)) + 
  facet_wrap(~windows) + 
  labs(
    title    = "Taxa Marginal de Substituição: Erro de Estimação vs. Erro de Especificação", 
    subtitle = "Ações do Índice Dow Jones - 2000-2021 - estimação em janelas móveis",
    caption  = "Fonte: Yahoo Finance / Pacote `YahooTickers`", 
    y        = NULL
    )

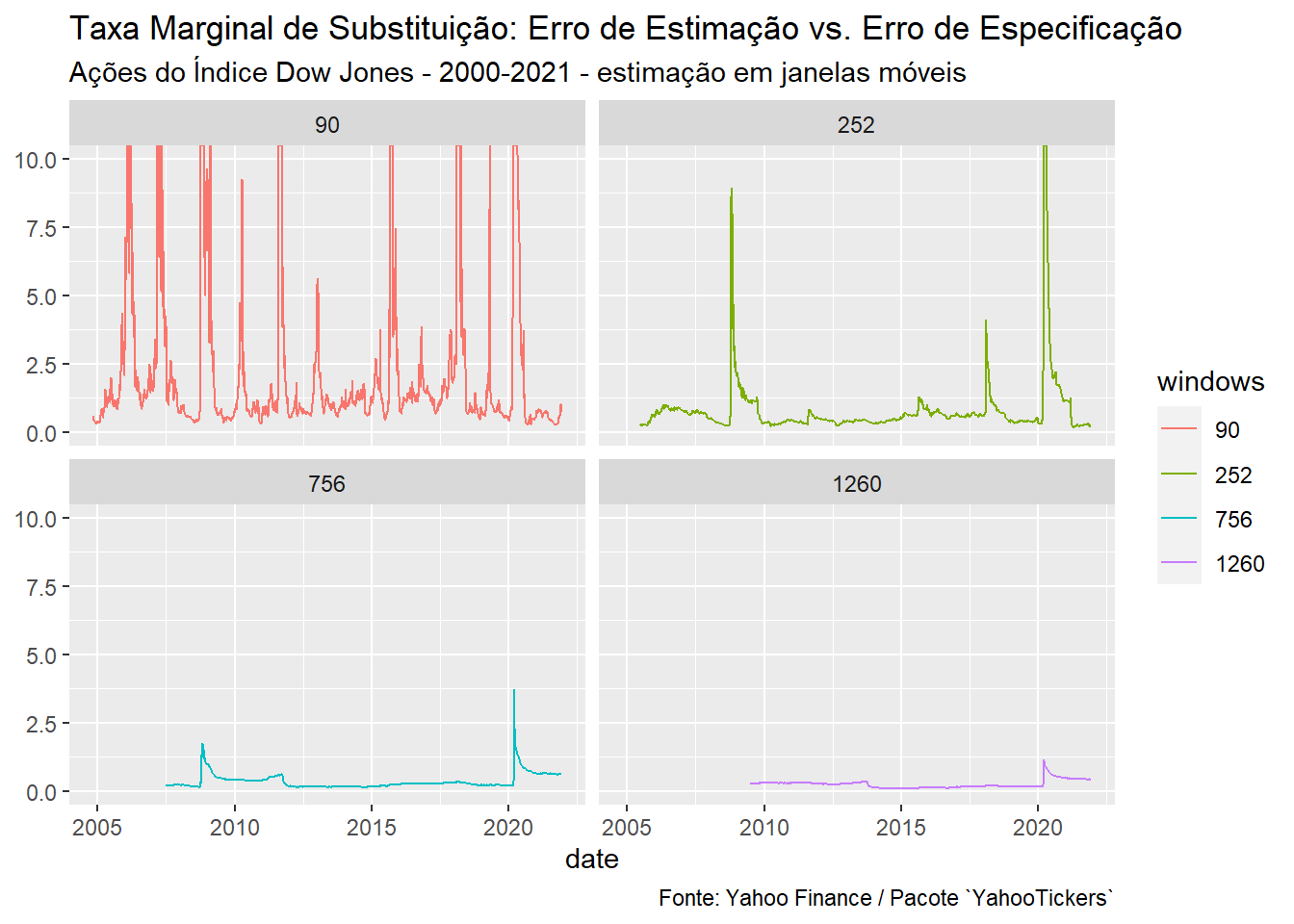
Sempre que a fração $ \frac{\delta}{1-\delta}$ for maior do que $1$ há pelo menos tanto erro de estimação na matrix amostral, quanto há viés na matrix estruturada, $F$ . Consequentemente, um maior $\delta$ é necessário para equalizar a relação entre viés e variância.

Monitorar essa taxa de troca pode ajudar o gestor a identificar quando adicionar mais estrutura ou dar aquele toque bayesiano na análise econométrica.

Assume-se que a soma dos erros ao quadrado (SEQ) seja utlizada como função de perda para determinar o “melhor” estimador. ↩︎
Você pode fazer o download do código original aqui. ↩︎
Se essa estrutura parece estranha para você, dê uma olhada na documentação da função rolling_origin: https://rsample.tidymodels.org/reference/rolling_origin.html. ↩︎